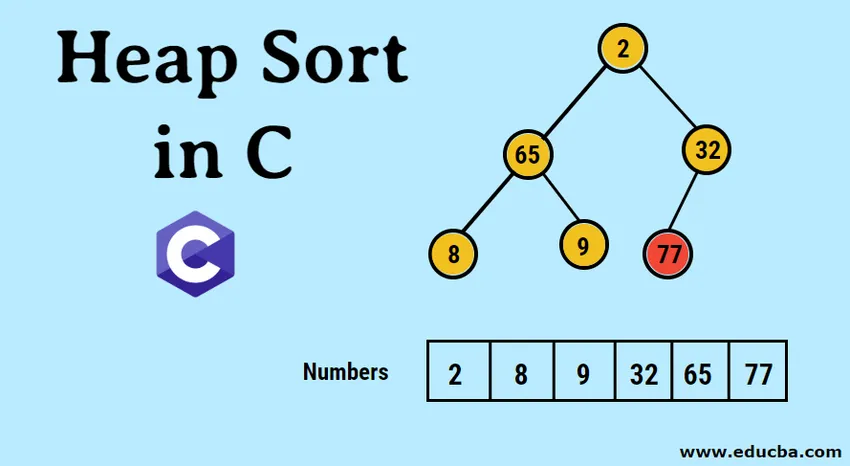
Sissejuhatus hunnikusorteerimisse C-s
Sorteerimine on tehnika, mille eesmärk on erinevate omaduste põhjal elementide järjestamine. (Atribuudid, nagu andmete järjestamine kasvavas, kahanevas või tähestikulises järjekorras). Üks suur näide sorteerimisest, millest siin mõelda saame, on esemete tellimine veebiostude ajal. Saame suhelda hindade, populaarsuse, uusimate ja nii edasi. Nii et elementide sorteerimisel positsioneerimiseks on palju tehnikaid. Selles teemas õpime C-s sortimise kohta C-s.
Siin õpime C-programmeerimiskeele kaudu ühte levinumat sorteerimistehnikat Heap Sort.
Hunnikute sortimise loogika
Kuidas tegelikult saame hunnikutes sorteerida? Vaatame allpool.
Esiteks on hunnik üks puupõhiseid andmestruktuure. Siin osalev puu on alati täielik kahendpuu. Ja hunnikuid on kahte tüüpi
- Min - Heap: üldiselt paigutatud kasvavas järjekorras, st kui vanema sõlmeelemendi väärtus on väiksem kui alamsõlme elementide väärtus.
- Max - Heap: üldjuhul kahanevas järjekorras, st kui vanema sõlmeelemendi väärtus on suurem kui alamsõlme elementide väärtus.
Sammud sorteerimiseks
- Kui sortimata loendiandmed on saadud, korraldatakse elemendid hunniku andmestruktuuris kas mini- või max-hunniku loomise põhjal.
- Esimene element ülaltoodud loendist lisatakse meie massiivi
- Jällegi moodustatakse peaandmete struktuuri tehnika, mis on sama nagu esimesel etapil, ja jälle võetakse kas meie massiivi kas kõrgeim või väikseim element.
- Korduvad toimingud aitavad meil sorteeritud loendiga massiivi saada.
Programm hunnikute sortimiseks C-s
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Esiteks palume kasutajal sisestada sorteerimiseks vajalike elementide arv ja seejärel lubatakse kasutajal sisestada erinevad sorteeritavad elemendid.
Järgmised sammud
- Järgmine, millele keskendume, on hunnikute massiivi, antud juhul maksimaalse hunniku massiivi loomine.
- Maksimaalse hunniku massiivi saamise peamine tingimus on kontrollida, kas ühegi vanema sõlme väärtus pole väiksem kui selle alamsõlme väärtus. Me vahetame, kuni selle tingimuse saavutame.
- Selle täieliku binaarse puu peamine eelis on see, et vanema sõlme vasakule ja paremale lapsesõlmele pääseb vastavalt väärtustega 2 (i) + 1 ja 2 * (i) + 2. Kus i on algsõlm.
- Niisiis paigutame siin oma juursõlme, mis sisaldab maksimaalset väärtust, kõige paremasse lehe sõlme. Ja siis jälle sama protseduuri järgides, nii et järgmisest maksimaalsest arvust saab nüüd juursõlm.
- Me jätkame sama protseduuri, kuni hunnikute massiivi on jäänud ainult üks sõlm.
- Ja siis korraldame oma hunnikute massiivi, et moodustada täiuslik sorteeritud massiiv kasvavas järjekorras.
- Lõpuks trükime väljundis sorteeritud massiivi.
Väljund:
Väljund on lisatud allpool.
Lubage mul näidata teile sündmuste piltlikku esitust:
- Sisestatud andmed esitatakse esmalt ühemõõtmelise massiivi kujul järgmiselt.

- Moodustatud binaarse puu piltlik kujutis on järgmine:
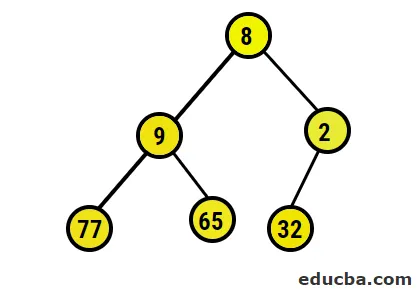
- Nüüd hakkame üle minema maksimaalsele kuhjale, veendudes, et kõik vanemsõlmed on alati suuremad kui lapsesõlmed. Nagu väljundis hunniku järgi sorteeritud massiivi all mainitud, oleks piltlik kujutis järgmine:
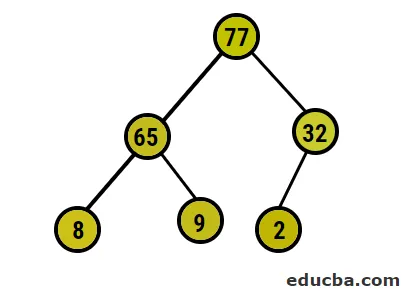
- Pärast seda vahetame juursõlme äärmise lehesõlmega ja kustutame selle seejärel puust. Lehesõlm oleks juur nüüd ja jälle sama protsess e, millele järgneb juure kõrgeima elemendi hankimine
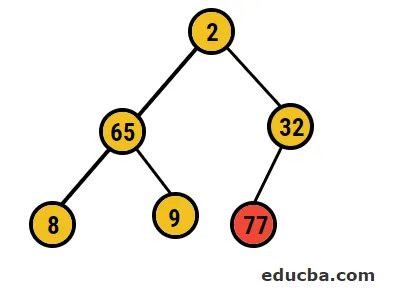
- Niisiis kustutatakse sellest puust 77 numbrit ja paigutatakse meie sorteeritud massiivi ning protsessi korratakse.
Ülalpool oleme seda näinud maksimaalse hunniku massiivi moodustamiseks. Sama protsessi käsitletakse ka min-hunniku massiivi moodustamisega. Nagu eespool arutatud, on ainus erinevus vanema ja lapsesõlme elementide suhetes.
Kas võite proovida harjutusharjutuste moodustamist kahanevas järjekorras?
Järeldus
Kuigi sorteerimistehnikaid on palju, peetakse hunnikute sorteerimist oma aja ja ruumi keerukuse tõttu üheks paremaks sorteerimistehnikaks. Kõigi parimate, keskmiste ja halvimate juhtude ajaline keerukus on O (nlogn), kus halvimal juhul on keerukus parem kui Quicksorti halvimal juhul ja ruumi keerukus on O (1).
Soovitatavad artiklid
See on juhend hunnikute sortimise kohta C. Siin käsitleme hunnikute sortimise loogikat ja toiminguid koos proovikoodi ja väljundiga koos piltlike esitustega. Võite lisateabe saamiseks vaadata ka järgmisi artikleid -
- Hunnik sorteerib Java
- Valik Sorteeri Java-s
- C-programmi palindroom
- C-programmeerimise mustrid
- Hunnikus sortimine C ++-s (algoritm)
- Hunnik sorteerimine Pythonis
- C Programmeerimismaatriksi korrutamine