Sissejuhatus hierarhilisse klastrisse
- Hiljuti palus üks meie klient meie meeskonnal tuua välja segmentide loend, mille järjekord on oluline nende klientide jaoks, et suunata nad ühe oma äsja turule lastud toote frantsiisi. Selgelt, kui klientide segmentimine osalise rühmitamise teel (k-keskmine, c-fuzzy) ei too selgelt esile tähtsuse järjekorda, kus pilt hierarhilisest klastrist tuleb.
- Hierarhiline klasterdamine eraldab andmed erinevatesse rühmadesse, tuginedes mõnele klastriteks tuntud sarnasuse mõõtmisele, mille põhieesmärk on klastrite vahelise hierarhia loomine. See on põhimõtteliselt juhendamata õpe ja sarnasuse mõõtmiseks atribuutide valimine on rakendusespetsiifiline.
Andmete klastri klaster
- Aglomeratiivne klasterdamine
- Jagav klasterdamine
Võtame näiteks andmed, hinded, mille 5 õpilast on saanud nende rühmitamiseks eelseisvaks võistluseks.
| Üliõpilane | Marks |
| A | 10 |
| B | 7 |
| C | 28 |
| D | 20 |
| E | 35ndad |
1. Aglomeratiivne klasterdamine
- Alustuseks käsitleme iga punkti / elemendi kaalu klastrina ja jätkame sarnaste punktide / elementide liitmist uue klastri moodustamiseks uuel tasemel, kuni me jääme ühte klastrisse alt üles lähenemisviisiga.
- Aglomeratiivse klastri moodustamise kaks populaarset näidet on ühtne ja täielik seos. Muud kui keskmine ja Centroidne ühendus. Ühendamisel ühendame igas astmes kaks klastrit, mille kahel lähimal liikmel on väikseim vahemaa. Täielikus ühenduses liidetakse väikseima vahemaa liikmed, mis annavad väikseima maksimaalse paarissuuna.
- Lähedusmaatriks, see on hierarhilise rühmituse teostamise tuum, mis annab iga punkti vahelise vahemaa.
- Tehkem tabelis esitatud andmete jaoks lähedusmaatriks, kuna arvutades punktide vahelise kauguse teiste punktidega, on see asümmeetriline maatriks kujuga n × n, meie puhul 5 × 5 maatriksid.
Populaarne meetod kauguse arvutamiseks on:
- Eukleidese vahemaa (ruut)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Manhattani vahemaa
dist((x, y), (a, b)) =|x−c|+|y−d|
Kõige sagedamini kasutatakse eukliidilist vahemaad, siin kasutame sama ja me läheme keeruka sidemega.
| Üliõpilane (klastrid) | A | B | C | D | E |
| A | 0 | 3 | 18 | 10 | 25 |
| B | 3 | 0 | 21 | 13 | 28 |
| C | 18 | 21 | 0 | 8 | 7 |
| D | 10 | 13 | 8 | 0 | 15 |
| E | 25 | 28 | 7 | 15 | 0 |
Lähedusmaatriksi diagonaalsed elemendid on alati 0, kuna sama punktiga punkti vaheline kaugus on alati 0, seega vabastatakse diagonaalsed elemendid grupeerimisest.
Siin, iteratsioonis 1, on väikseim vahemaa 3, seega ühendame A ja B klastri moodustamiseks, moodustades taas klastri (A, B) uue lähedusmaatriksi, võttes (A, B) klastri punkti 10, st maksimaalselt ( 7, 10), nii et äsja moodustatud lähedusmaatriks oleks
| Klastrid | (A, B) | C | D | E |
| (A, B) | 0 | 18 | 10 | 25 |
| C | 18 | 0 | 8 | 7 |
| D | 10 | 8 | 0 | 15 |
| E | 25 | 7 | 15 | 0 |
Korduses 2, 7 on minimaalne vahemaa, seega liites C ja E moodustades uue klastri (C, E), korratakse korramist, mida järgiti iteratsioonis 1, kuni jõuame ühe klastrini, siin peatume 4. iteratsioonis.
Kogu protsess on kujutatud allpool toodud joonisel:
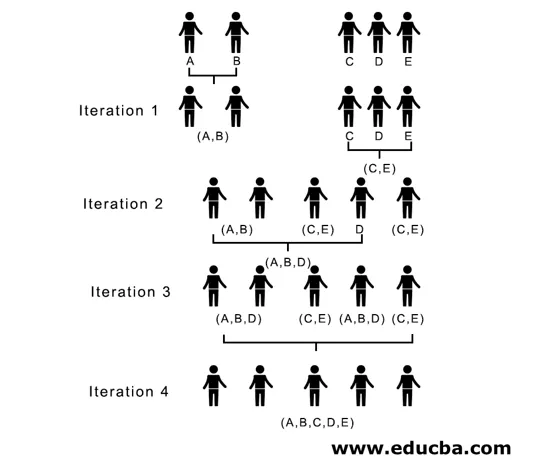
(A, B, D) ja (D, E) on kaks iteratsiooni 3 moodustunud klastrit, viimases iteratsioonis näeme, et oleme jäänud ühte klastrisse.
2. Jagav klasterdamine
Alustuseks käsitleme kõiki punkte ühe klastrina ja eraldame need kõige kaugema vahemaa tagant, kuni lõpetame üksikute punktidega üksikute klastritega (mitte tingimata, et keskel võime peatuda, sõltub minimaalsest elementide arvust, mida me igas klastris tahame) igal sammul. See on vastupidine aglomeratiivsele klastritele ja see on ülalt alla suunatud lähenemisviis. Jagavad rühmitused on viis, kuidas korduv k tähendab rühmitamist.
Aglomeratiivse ja jagatava klastri vahel valimine sõltub jällegi rakendusest, kuid siiski tuleb arvestada järgmiste punktidega:
- Jagunemine on keerulisem kui aglomeratiivne klasterdamine.
- Jagatud rühmitamine on tõhusam, kui me ei loo täielikku hierarhiat üksikute andmepunktide alla.
- Aglomeratiivne rühmitus langetab otsuse kohalike kaalutluste kaalumisel, võtmata arvesse globaalseid suundumusi, mida esialgu ei saa ümber pöörata.
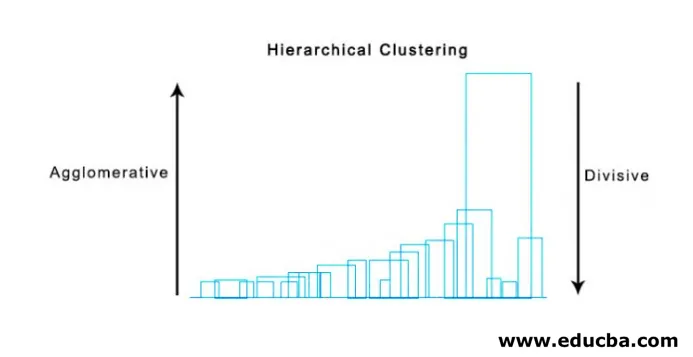
Hierarhilise klastri visualiseerimine
Äärmiselt kasulik meetod hierarhilise klastri visualiseerimiseks on Dendogram. Dendogrammid on puusarnased struktuurid, mis registreerivad ühinemiste ja lõhede jada, kus vertikaalne joon tähistab klastrite vahelist kaugust, vertikaaljoonte vaheline kaugus ja klastrite vaheline kaugus on otseselt proportsionaalne, st mida rohkem seda vahemaad, mida klastrid on tõenäoliselt erinevad.
Klastrite arvu määramiseks saame kasutada dendogrammi, lihtsalt tõmmake sirge, mis ristub dendogrammil pikima vertikaalse joonega; mitu ristuvat vertikaalset joont on vaadeldud klastrite arv.
Allpool on näide Dendogrammist.
Seal on üsna lihtsad ja otsesed python-paketid ning selle funktsioonid on hierarhilise rühmituse teostamiseks ja dendogrammide joonistamiseks.
- Hierarhia skipist.
- Cluster.hierarchy.dendogram visualiseerimiseks.
Ühised stsenaariumid, milles kasutatakse hierarhilist rühmitust
- Klientide segmenteerimine toodete või teenuste turundamiseks.
- Linnaplaneerimine ehitiste / teenuste / hoonete ehitamise kohtade kindlaksmääramiseks
- Sotsiaalse võrgustiku analüüs näiteks tuvastage kõik MS Dhoni fännid, kes reklaamiksid tema biopilti.
Hierarhilise klastri eelised
Eelised on toodud allpool:
- Osalise rühmitamise korral nagu k-vahendid peaksid klastrite arv olema teada enne rühmitamist, mis pole praktilistes rakendustes võimalik, samas kui hierarhilises klastrites pole klastrite arvu eelnev teadmine vajalik.
- Hierarhiline klasterdamine väljastab hierarhia, st informatiivsema struktuuri kui osalise klasterdamise teel tagastatud lamedate klastrite struktureerimata kogum.
- Hierarhilist rühmitust on lihtne rakendada.
- Toob välja enamiku stsenaariumide tulemused.
Järeldus
Klasterdamise tüüp teeb andmete esitamisel suure erinevuse. Hierarhiline klasterdamine on informatiivsem ja hõlpsamini analüüsitav, eelistatavam kui osaline klasterdamine. Ja seda seostatakse sageli soojakaartidega. Unustamata sarnasuse või erinevuse arvutamiseks valitud atribuute, mõjutab valdavalt nii klastrid kui ka hierarhia.
Soovitatavad artiklid
See on juhend Hierarhilise klastrimise kohta. Siin käsitleme hierarhilise klastri kasutuselevõttu, eeliseid ja tavalisi stsenaariume, milles hierarhilist klastrit kasutatakse. Lisateavet leiate ka meie muudest soovitatud artiklitest -
- Klasterdamisalgoritm
- Klastrid masinõppes
- Hierarhiline rühmitus R-s
- Klastrimismeetodid
- Kuidas eemaldada tabelist hierarhia?