
Sissejuhatus binoomjaotusesse R
See artikkel kirjeldab, kuidas kasutada R-s binoomjaotusi väheste tõenäosusjaotusega seotud toimingute jaoks. Ärianalüüs kasutab keeruka probleemi jaoks binoomide tõenäosust. R-l on arvukalt sisseehitatud funktsioone statistilistes häiretes kasutatavate binoomjaotuste arvutamiseks. Binoomjaotus, mida nimetatakse ka Bernoulli katseteks, võtab kahte tüüpi edukuse p ja ebaõnnestumise S. Binoomjaotuse mudeli peamine eesmärk on see, et nad arvutaksid välja võimalikud tõenäosuse tulemused, jälgides konkreetset arvu positiivseid võimalusi, korrates protsessi teatud arv kordi. . Neil peaks olema kaks võimalikku tulemust (edu / ebaõnnestumine), seetõttu on tulemus dihhotoomiline. Eelnevalt määratletud matemaatiline märge on p = edukus, q = 1-p.
Binoomjaotustega on seotud neli funktsiooni. Need on dbinom, pbinom, qbinom, rbinom. Vormindatud süntaks on esitatud allpool:
Süntaks
- dbinom (x, suurus, prob)
- pbinom (x, suurus, prob)
- qbinom (x, suurus, prob) või qbinom (x, suurus, prob, lower_tail, log_p)
- rbinom (x, suurus, prob)
Funktsioonil on kolm argumenti: väärtus x on kvantide vektor (0 kuni n), suurus on jälgimiskatsete arv, prob tähistab iga katse tõenäosust. Vaatame ükshaaval näitega.
1) dbinom ()
See on tiheduse või jaotusfunktsioon. Vektorväärtused peavad olema täisarv, see ei tohiks olla negatiivne arv. See funktsioon proovib leida mitu edu punktile nr. katsetest, mis on fikseeritud.
Binoomjaotus võtab suuruse ja x väärtused. näiteks suurus = 6, on võimalikud x väärtused 0, 1, 2, 3, 4, 5, 6, mis tähendab P (X = x).
n <- 6; p<- 0.6; x <- 0:n
dbinom(x, n, p)
Väljund:
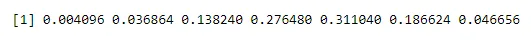
Tehes tõenäosuse ühele
n <- 6; p<- 0.6; x <- 0:n
sum(dbinom(x, n, p))
Väljund:
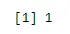
Näide 1 - haigla andmebaas näitab, et 65% vähktõbe põdevatest patsientidest sureb see. Milline on tõenäosus, et viiest juhuslikult valitud patsiendist, kellest 3 taastub?
Siin rakendame dbinomi funktsiooni. Tõenäosus, et 3 taastub, kasutades tiheduse jaotust kõigis punktides.
n = 5, p = 0, 65, x = 3
dbinom(3, size=5, prob=0.65)
Väljund:

X väärtuse 0 kuni 3 korral:
dbinom(0, size=5, prob=0.65) +
+ dbinom(1, size=5, prob=0.65) +
+ dbinom(2, size=5, prob=0.65) +
+ dbinom(3, size=5, prob=0.65)
Väljund:
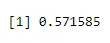
Järgmisena looge 40 paberist koosnev valim, mida suurendatakse kahega, luues dinoomi abil ka binoomi.
a <- seq(0, 40, by = 2)
b <- dbinom(a, 40, 0.4)
plot(a, b)
Pärast ülaltoodud koodi täitmist saadakse järgmine väljund: Binoomjaotus joonistatakse graafiku abil, kasutades funktsiooni plot ().
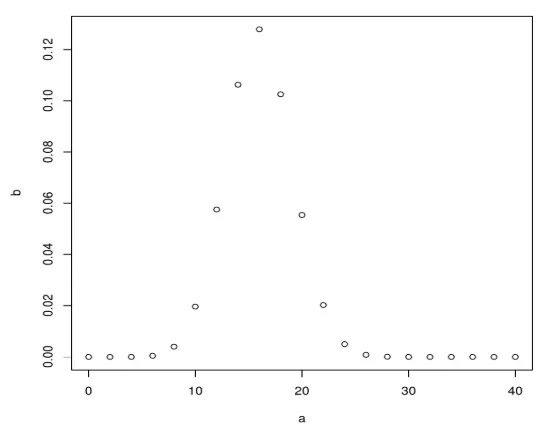
Näide 2 - Vaatleme stsenaariumi, oletame, et tõenäosus, et õpilane laenutab raamatukogust raamatut, on 0, 7. Raamatukogus on 6 õpilast, mis on tõenäosus, et 3 neist laenutab raamatut?
siin P (X = 3)
Kood:
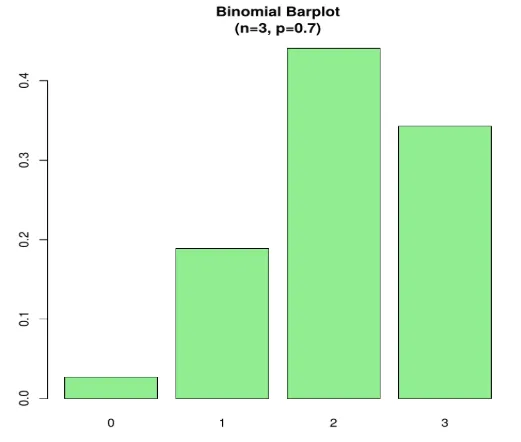
n=3; p=.7; x=0:n; prob=dbinom(x, n, p);
barplot(prob, names.arg = x, main="Binomial Barplot\n(n=3, p=0.7)", col="lightgreen")
Allpool Joonis on näha, kui p> 0, 5, seetõttu on binoomi jaotus kuvaril positiivselt kaldu.
Väljund:
2) Pbinom ()
arvutab binoomi või CDF kumulatiivsed tõenäosused (P (X <= x)).
Näide 1:
x <- c(0, 2, 5, 7, 8, 12, 13)
pbinom(x, size=20, prob=.2)
Väljund:

Näide 2: Dravid lööb kaalu langetades värava 20% -l katsest. Kui ta vibutab 5 korda, siis kui suur on tõenäosus, et ta saab 4 või väiksema värava?
Edu tõenäosus on siin 0, 2 ja 5 katse jooksul saame
pbinom(4, size=5, prob=.2)
Väljund:
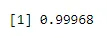
Näide 3: 4% ameeriklastest on mustanahalised. Leidke 2 musta õpilase tõenäosus, kui valite juhuslikult 6 õpilast 100 klassist ilma asendamiseta.
Kui R: x = 4 R: n = 6 R: p = 0 0 4
pbinom(4, 6, 0.04)
Väljund: -
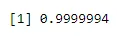
3) qbinom ()
See on kvantitatiivne funktsioon ja teeb kumulatiivse tõenäosusfunktsiooni pöördvõrdeliselt. Kumulatiivne väärtus langeb kokku tõenäosusväärtusega.
Näide: kui paljudel sabadel on tõenäosus 0, 2, kui mündi visatakse 61 korda.
a <- qbinom(0.2, 61, 1/2)
print(a)
Väljund: -
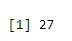
4) rbinom ()
See genereerib juhuslikke numbreid. Erinevad tulemused annavad erineva juhusliku väljundi, mida kasutatakse simulatsiooniprotsessis.
Näide: -
rbinom(30, 5, 0.5)
rbinom(30, 5, 0.5)
Väljund: -

Iga kord, kui seda teostame, annab see juhuslikke tulemusi.
rbinom(200, 4, 0.4)
Väljund: -

Siin teeme seda, eeldades, et ühe mündivõtmise tulemus on 30 mündi.
rbinom(30, 1, 0.5)
Väljund: -
Kasutades barplot:
a<-rbinom(30, 1, 0.5)
print(a)
barplot(table(a),>
Väljund: -
Edukuse keskmise leidmiseks
output <-rbinom(10, size=60, 0.3)
mean(output)
Väljund: -
Järeldus - binoomne jaotus R-s
Seetõttu oleme selles dokumendis arutanud binoomide jaotuse R-s. Oleme R stuudios ja R-koodilõikudes erinevaid näiteid simuleerinud ja kirjeldanud ka sisseehitatud funktsioone, mis aitavad genereerida binoomiarvutusi. Binoomjaotuse arvutamisel R kasutatakse statistilisi arvutusi. Seetõttu aitab binoomjaotus leida tõenäosust ja juhuslikku otsingut binoommuutuja abil.
Soovitatavad artiklid
See on juhend Binomaalse jaotuse kohta R-s. Siin on käsitletud sissejuhatust ja selle funktsioone, mis on seotud Binomiaalse jaotusega, koos süntaksi ja sobivate näidetega. Lisateavet leiate ka meie muudest soovitatud artiklitest -
- Binomiaalse jaotuse valem
- Majandus vs äri
- Ärianalüütika tehnikad
- Linuxi distributsioonid