
Aritmeetiline keskmine valem (sisukord)
- Valem
- Näited
- Kalkulaator
Mis on aritmeetiline keskmine valem?
Mõiste “aritmeetiline keskmine” viitab põhimõtteliselt kahe või enama arvu matemaatilisele keskmisele. Kuid aritmeetilise keskmise arvutamise meetod võib varieeruda sõltuvalt andmekogumi iga muutuja sagedusest - lihtne keskmine (võrdselt kaalutud) või kaalutud keskmine. Võrdse kaaluga muutujate aritmeetilise keskmise valemi saab tuletada, summeerides kõik andmekogumis olevad muutujad ja jagades seejärel tulemuse muutujate arvuga. Matemaatiliselt tähistatakse seda järgmiselt:
Arithmetic Mean = (x 1 + x 2 + …. + x n ) / n
või
Arithmetic Mean =∑ x i / n
Kus,
- x i = i muutuja
- n = muutujate arv andmekogumis
Ebavõrdselt kaalutud muutujate korral saab aritmeetilise keskmise valemi tuletada, summeerides iga muutuja korrutise ja selle sageduse ning seejärel jagatakse tulemus sageduste summaga. Matemaatiliselt tähistatakse seda järgmiselt:
Arithmetic Mean = (f 1 *x 1 +f 2 *x 2 + …. + f n *x n ) / (f 1 + f 2 + ….. + f n )
või
Arithmetic Mean = ∑ (f i * x i ) / f i
Kus
- x i = i muutuja
- f i = i- nda muutuja sagedus
Aritmeetilise keskmise valemi näited (Exceli malliga)
Võtame näite, et aritmeetilise keskmise arvutamist paremini mõista.
Selle aritmeetilise keskmise valemi Exceli malli saate alla laadida siit - aritmeetilise keskmise valemi Exceli mallAritmeetiline keskmine valem - näide # 1
Võtame näiteks lööja, kes tegi viimase aasta jooksul 10 järgmise mänguaja jooksul järgmised jooksud: 45, 65, 7, 10, 43, 35, 25, 17, 78, 91. Laske välja lööja keskmine tema viimases 10 kõrtsi.
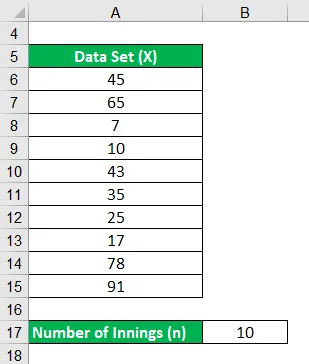
Lahendus:
Aritmeetiline keskmine arvutatakse järgmise valemi abil
Aritmeetiline keskmine = ∑ x i / n
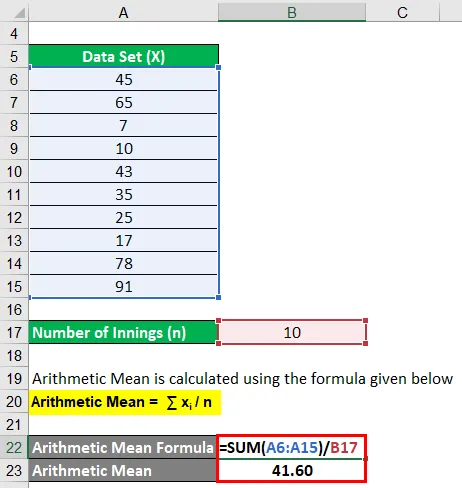
- Aritmeetiline keskmine = (45 + 65 + 7 + 10 + 43 + 35 + 25 + 17 + 78 + 91) / 10
- Aritmeetiline keskmine = 41, 60
Seetõttu jäi lööja keskmiseks viimase 10 kõnnaku jooksul keskmiseks 41, 60 tiiru per inning.
Aritmeetiline keskmine valem - näide # 2
Võtame näite klassist, kus on 45 õpilast. Hiljuti korraldati loodusteaduste jaoks iganädalane test, milles õpilasi hinnati skaalal 1 kuni 10. Arvutage järgmise teabe põhjal testi keskmised hinded.
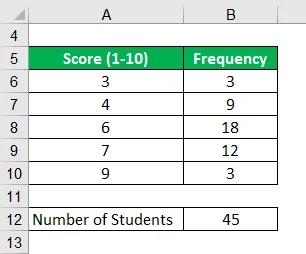
Lahendus:
Aritmeetiline keskmine arvutatakse järgmise valemi abil
Aritmeetiline keskmine = ∑ (f i * x i ) / f i
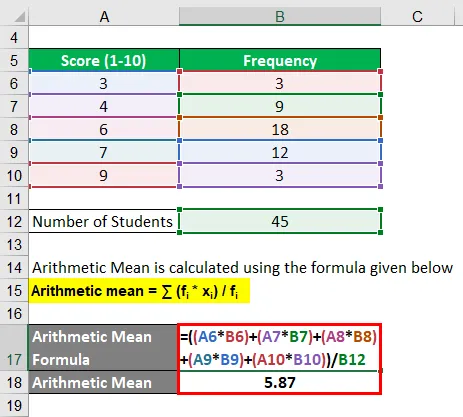
- Aritmeetiline keskmine = ((3 * 3) + (4 * 9) + (6 * 18) + (7 * 12) + (9 * 3)) / 45
- Aritmeetiline keskmine = 264/45
- Aritmeetiline keskmine = 5, 87
Seetõttu oli klassi keskmine punktisumma looduskatsel 5, 87.
Aritmeetiline keskmine valem - näide # 3
Võtame näite kahest andmekogumist, millel on kaks erinevat aritmeetilist keskmist. Esimeses andmekogumis on 10 muutujat keskmisega 45, teises andmekogumis 7 muutujaga ja keskmisega 42. Määrake kahe andmekogumi kombineeritud aritmeetiline keskmine.
Lahendus:
Kombineeritud andmekogumi aritmeetilised vahendid arvutatakse järgmise valemi abil
Aritmeetiline keskmine = ((m 1 * n 1 ) + (m 2 * n 2 )) / (n 1 + n 2 )
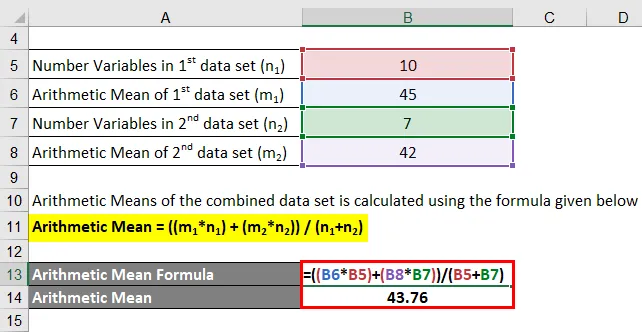
- Aritmeetiline keskmine = (45 * 10 + 42 * 7) / (10 + 7)
- Aritmeetiline keskmine = 43, 76
Seetõttu on kombineeritud andmekogumi aritmeetiline keskmine 43, 76.
Seletus
Aritmeetilise keskmise valemi saab arvutada järgmiste sammude abil:
1. samm: kõigepealt koguge ja sorteerige muutujad, mille jaoks tuleb arvutada aritmeetiline keskmine. Muutujaid tähistatakse x i-ga .
2. samm. Seejärel määrake andmekogumis muutujate arv ja võrdselt kaalutud muutujate korral tähistatakse seda numbriga n. Vastasel juhul selgitage välja iga muutuja sagedus ja neid tähistatakse f i-ga ning muutujate arv on sageduste liitmine.
3. samm: Lõpuks saab võrdselt kaalutud muutujate aritmeetilise keskmise valemi tuletada, lisades kõik muutujad, ja siis jagatakse tulemus andmekogumis olevate muutujate arvuga, nagu allpool näidatud.
Aritmeetiline keskmine = ∑ x i / n
Kaalutud keskmise korral saab aritmeetilise keskmise valemi siiski tuletada, summeerides iga muutuja korrutise ja selle sageduse ning seejärel jagatakse tulemus sageduste summaga, nagu allpool näidatud.
Aritmeetiline keskmine = ∑ f i * x i / f i
Aritmeetilise keskmise valemi olulisus ja kasutamine
Aritmeetilise keskmise mõiste on väga lihtne ja elementaarne. Kuid see on endiselt väga oluline, kuna seda kasutatakse sageli statistilise näitajana, et hinnata andmekogumis keskmist tulemust. Tegelikult võimaldab see hinnata, millised muutujatest on paremad või madalamad kui rühma keskmised. Seda kasutatakse ka mõõtühikuna, et esitada kogu andmeseeria keskmine väärtus. Lisaks kasutatakse aritmeetilist keskmist juhtudel, kui geomeetriline keskmine või harmooniline väärtus on vähem kasulikud, näiteks keskmine klass, kaal jne.
Aritmeetilise keskmise valemi kalkulaator
Võite kasutada järgmist aritmeetilist keskmise kalkulaatorit
| x 1 | |
| x 2 | |
| x 3 | |
| x 4 | |
| n | |
| Aritmeetiline keskmine | |
| Aritmeetiline keskmine | = |
|
|
Soovitatavad artiklid
See on aritmeetilise keskmise valemi juhend. Siin käsitleme kuidas arvutada aritmeetilist keskmist koos praktiliste näidetega. Pakume ka allalaaditava excelimalli abil aritmeetilist keskmist kalkulaatorit. Lisateabe saamiseks võite vaadata ka järgmisi artikleid -
- Kuidas arvutada harmoonilist keskmist?
- Rahvastiku keskmise valemi juhend
- Keskmise arvutamine valemi abil
- Netomüügi valemi näited