
Erinevus Z-skoori ja T-skoori vahel
Z-skoor on töötlemata andmete teisendamine standardseks skooriks, kui teisendus põhineb populatsiooni keskmisel ja populatsiooni standardhälbel. Kui täielik andmekogum on meiega saadaval, saame Z-punkti arvutada. Z skoor on populatsiooni keskmise lahutamine töötlemata skoorist ja seejärel jagatakse tulemus populatsiooni standardhälbega. T-skoor on töötlemata andmete teisendamine standardseks skooriks, kui teisendus põhineb valimi keskmisel ja valimi standardhälbel. Kui rahvastikukogum pole kättesaadav, peame valimi keskmise ja populatsiooni standardhälbe arvutamiseks koguma mõned valimisandmed.
Z skoor
Normaalse jaotuse korral, kus on olemas täielikud andmed, on see kaugus keskmisest. Selle valem on järgmine:
Z= (x-μ)/σ
Kus,
X = üksikud töötlemata andmed
μ = populatsiooni keskmine
σ = populatsiooni standardhälve
T skoor
T-tulemus on üksikute standardhälvete lahutamine keskmistest keskmistest ja jagatakse tulemus valimi standardhälbega, mis on korrutatud valimi suurusega. Selle valem on järgmine:
t = ((- μ)/s)*
= proovi keskmine
μ = populatsiooni keskmine
s = proovi standardhälve
n = valimi suurus
Võtame näite, et seda paremini mõista:
Töös on 3 alajaotist - I, II ja III. Las ma vastan õigesti 25% õpilaste arvust, st 75% ei suuda sellele õigesti vastata. Samamoodi laske 10% ja 20% II ja III jaotisele õigesti vastanud inimeste arvust, seega on 90% ja 80% leidnud II ja III jaotise. Eeldame, et nende kolme elemendi abil mõõdetud võime on sama ja see on tavaliselt jaotunud,
Klassi iga õpilase tulemust kasutatakse punktide keskmise arvutamiseks, mis on võrdne 50-ga ja standardhälbega 10. Võime Z-hinde arvutada tulemusega 50 kui (50-50) / 10 = 0
Saame tõlgendada seda, et õpilase tulemus on 0 kaugust (standardhälbe ühikutes) keskmisest, seega on õpilase hinne keskmine.
Kui skoor on 60, on Z skoor (60-50) / 10 = 1
Saame tõlgendada, et õpilase tulemus on keskmisest kõrgem - 1 standardhälbe kaugus keskmisest kõrgem.
Z-punkti ja T-punkti võrdlus (infograafika)
Allpool on toodud 9 parima tulemuse erinevus Z-skoori vs T-skoori vahel 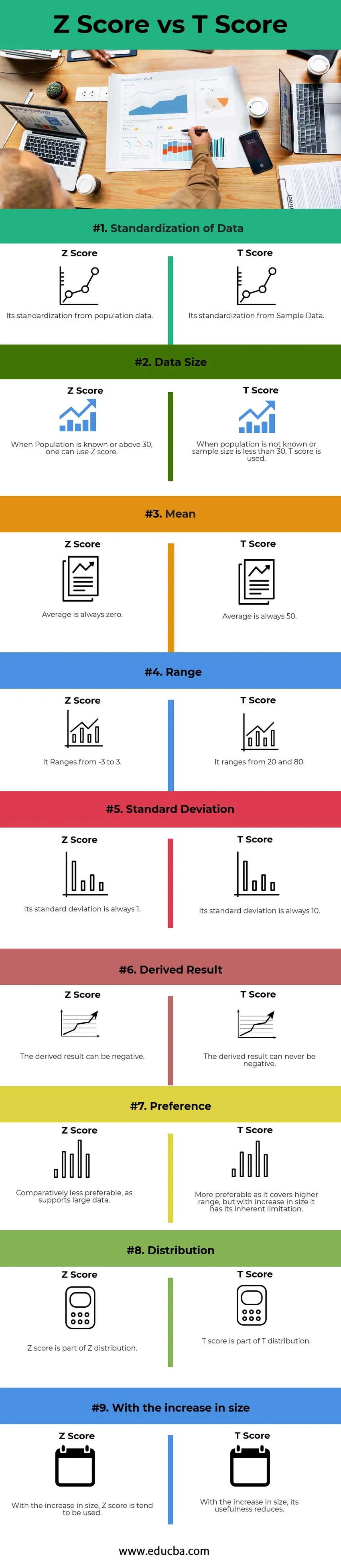
Peamised erinevused Z-skoori ja T-skoori vahel
Arutame mõned peamised erinevused Z-punkti ja T-punktide vahel
- Z-skoor on normeerimine rahvastiku töötlemata andmete või enam kui 30 valimisandme põhjal standardse skooriga, T-skoor on normeerimine valimi andmetega, mis on vähem kui 30, standardse skoorini
- Z skoor on vahemikus -3 kuni 3, T-skoor aga vahemikus 20 kuni 80.
- Kuna andmete suurus suureneb, kipub jaotus olema Z-jaotus. Mõlemad Z-skoori ja T-skoori jaotused on osa normaaljaotusest, kuid suuruse põhjal erinevad nad üksteisest
- Praktiliselt kasutatakse Z-punkti börsiandmetes ja ettevõtte pankrotti mineku võimaluste kontrollimiseks laialdaselt, t-punkti kasutatakse laialdaselt luude mineraaltiheduse ja luumurdude riski hindamisel.
Z skoor vs T skooride võrdlustabel
Vaatame 9 parimat Z-punkti ja T-punkti võrdlust
| Sr. | Võrdluspunktid | Z skoor | T skoor |
| 1 | Andmete standardimine | Selle standardiseerimine rahvastiku andmete põhjal | Selle standardiseerimine prooviandmete põhjal |
| 2 | Andmete suurus | Kui populatsioon on teada või üle 30, võib kasutada Z-punkti | Kui populatsiooni ei ole teada või kui valimi suurus on alla 30, kasutatakse T-punkti. |
| 3 | Tähendab | Keskmine on alati null. | Keskmine on alati 50. |
| 4 | Vahemik | See jääb vahemikku -3 kuni 3. | See on vahemikus 20 ja 80. |
| 5 | Standardhälve | Selle standardhälve on alati 1 | Selle standardhälve on alati 10 |
| 6 | Tuletatud tulemus | Tuletatud tulemus võib olla negatiivne | Tuletatud tulemus ei saa kunagi olla negatiivne |
| 7 | Eelistus | Võrdlemisi vähem eelistatav, kuna toetab suurandmeid | Eelistatavam, kuna see hõlmab suuremat vahemikku, kuid suuruse suurenemisega kaasneb sellele iseloomulik piirang |
| 8 | Levitamine | Z tulemus on osa Z jaotusest | T-skoor on osa T-jaotusest |
| 9 | Suuruse suurenemisega | Suuruse suurenemisega kiputakse kasutama Z-skoori | Suuruse suurenemisega väheneb selle kasulikkus. |
Järeldus
Mõlemad Z-skoor vs T-skoor on osa hüpoteesi testimisest normaaljaotuse korral. Kui teil on Z-skooride abil erinevate mõõtmistulemite komplekt, saate öelda, kuidas hinded jaotatakse. Siis saate neid võrrelda. Hinnete standardiseerimine on laialdaselt kasutatav protseduur teadusuuringute ja planeerimise valdkonnas, kuna need aitavad erinevate testide hindeid võrrelda. Hinnete standardiseerimine enne nende ühendamist aitab teadlasel saada paremaid ja võrreldavaid tulemusi.
Soovitatavad artiklid
See on juhend Z-punktide ja T-punktide suurima erinevuse kohta. Siin käsitleme ka Z-punkti vs T-punkti peamisi erinevusi infograafika ja võrdlustabeliga. Võite lisateabe saamiseks vaadata ka järgmisi artikleid -
- Rahandus vs majandus - suurim erinevus
- Puudujääk vs võlg - kumb on parem
- Vara ost vs aktsia ost
- Rahaturg vs kapitaliturg
- Altmani Z tulemuse ülevaade