
Sissejuhatus tuumameetoditesse
Tuumad või kerneli meetodid (nimetatakse ka kerneli funktsioonideks) on erinevat tüüpi algoritmid, mida kasutatakse mustri analüüsimiseks. Neid kasutatakse mittelineaarse probleemi lahendamiseks lineaarse klassifikaatori abil. Tuumade meetodeid kasutatakse SVM-is (Support Vector Machines), mida kasutatakse klassifitseerimise ja regressiooniprobleemide lahendamisel. SVM kasutab nn kerneli trikki, kus andmeid muudetakse ja leitakse võimalike väljundite jaoks optimaalne piir.
Kernelmeetodi vajadus ja selle toimimine
Enne kui alustame kernelmeetodite kasutamist, on olulisem mõista tugivektorimasinaid või SVM-e, kuna tuumasid rakendatakse SVM-i mudelites. Nii on tugivektorimasinad juhendatavad masinõppe algoritmid, mida kasutatakse klassifitseerimise ja regressiooniprobleemide korral, näiteks õuna klassifitseerimine puuvilja klassile, samas kui lõvi klassiloomad.
Allpool on näidatud, kuidas tugivektorimasinad välja näevad:
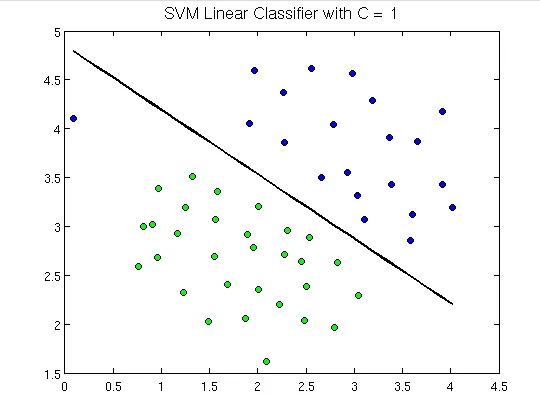
Siin näeme hüpertasandit, mis eraldab rohelisi punkte sinistest. Hüpertasapind on üks mõõde väiksem kui ümbritsev tasand. Näiteks ülaltoodud joonisel on meil kahemõõtmeline ruum, mis tähistab ümbritsevat ruumi, kuid ruumi eraldav või klassifitseeriv üksik on ümbritsevast ruumist üks mõõde väiksem ja seda nimetatakse hüpertasapinnaks.
Aga mis siis, kui meil on selline sisend:
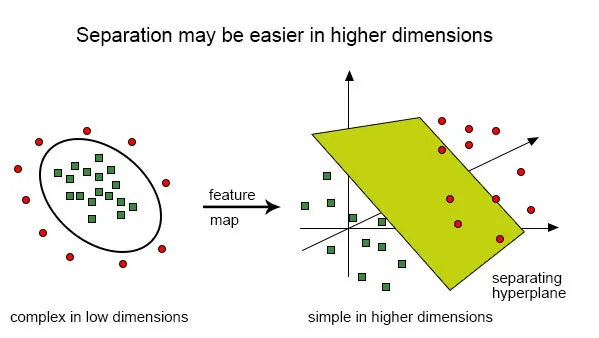
Seda klassifikatsiooni on lineaarse klassifikaatori abil väga keeruline lahendada, kuna puudub hea lineaarne joon, mis peaks punaseid ja rohelisi punkte klassifitseerima, kuna punktid on juhuslikult jaotatud. Siin tuleb kasutada kerneli funktsiooni, mis viib punktid kõrgematesse mõõtmetesse, lahendab seal tekkinud probleemi ja tagastab väljundi. Mõeldes sellele niimoodi, näeme, et rohelised punktid on mõnes perimeetri piirkonnas suletud, samas kui punased asuvad väljaspool seda, samuti võib olla ka muid stsenaariume, kus rohelised punktid võivad jaotada trapetsi kujuga ala.
See, mida me teeme, on teisendada kahemõõtmeline tasapind, mille klassifitseeris esmalt ühemõõtmeline hüpertasapind (või sirgjoon), kolmemõõtmeliseks alaks ja siin ei saa meie klassifikaator st hüpertasapind sirgjoonena, vaid kaheks -dimensiooniline tasand, mis lõikab ala.
Tuuma matemaatilisest mõistmisest mõistame Lili Jiangi tuuma võrrandit, mis on järgmine:
K (x, y) = kus,
K on kerneli funktsioon,
X ja Y on mõõtmete sisendid,
f on kaart n-mõõtmelisest m-mõõtmelisest ruumist ja,
on punkttoode.
Illustratsioon näite abil.
Ütleme nii, et meil on kaks punkti, x = (2, 3, 4) ja y = (3, 4, 5)
Nagu nägime, K (x, y) =.
Laskem kõigepealt arvutada
f (x) = (x1x1, x1x2, x1x3, x2x1, x2x2, x2x3, x3x1, x3x2, x3x3)
f (y) = (y1y1, y1y2, y1y3, y2y1, y2y2, y2y3, y3y1, y3y2, y3y3)
nii,
f (2, 3, 4) = (4, 6, 8, 6, 9, 12, 8, 12, 16) ja
f (3, 4, 5) = (9, 12, 15, 12, 16, 20, 15, 20, 25)
nii punkttoode,
f (x). f (y) = f (2, 3, 4). f (3, 4, 5) =
(36 + 72 + 120 + 72 +144 + 240 + 120 + 240 + 400) =
1444
Ja
K (x, y) = (2 * 3 + 3 * 4 + 4 * 5) 2 = (6 + 12 + 20) 2 = 38 * 38 = 1444.
Nagu me teada saime, annavad f (x) .f (y) ja K (x, y) meile sama tulemuse, kuid kunagine meetod nõudis palju arvutusi (3 mõõtme projekteerimise tõttu 9 mõõtmesse), kasutades kernel, see oli palju lihtsam.
Tuuma tüübid ja meetodid SVM-is
Vaatame mõnda tuumafunktsiooni või tüüpi, mida SVM-is kasutatakse:
1. Liner Kernel - Ütleme nii, et meil on kaks vektorit nimega x1 ja Y1, siis defineeritakse lineaarne tuum nende kahe vektori punkti korrutisega:
K (x1, x2) = x1. x2
2. Polünoomne tuum - Polünoomne tuum määratletakse järgmise võrrandiga:
K (x1, x2) = (x1, x2 + 1) d,
Kus,
d on polünoomi aste ja x1 ja x2 on vektorid
3. Gaussi tuum - see tuum on näide radiaalsest alusfunktsioonist koosnevas tuumas. Allpool on esitatud selle võrrand:
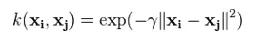
Antud sigmal on Gaussi tuuma jõudluses väga oluline roll ning seda ei tohiks ülehinnata ega alahinnata, seda tuleks vastavalt probleemile hoolikalt häälestada.
4. Eksponentsiaalne tuum - see on tihedas seoses eelmise tuumaga, st Gaussi tuumaga, mille ainus erinevus on - normi ruut eemaldatakse.
Eksponentsiaalse funktsiooni funktsioon on:
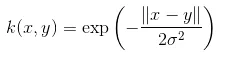
See on ka radiaalse aluse tuuma funktsioon.
5. Laplacian Kernel - seda tüüpi tuuma on vähem altid muudatustele ja see on täiesti võrdne eelnevalt käsitletud eksponentsiaalse funktsiooni kerneliga, Laplacianuse tuuma võrrand on esitatud järgmiselt:
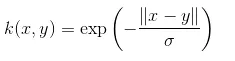
6. Hüperboolne ehk Sigmoid Kernel - seda tuuma kasutatakse masinõppe neuraalvõrgu piirkondades. Sigmoidituuma aktiveerimisfunktsioon on bipolaarne sigmoidfunktsioon. Hüperboolse kerneli funktsiooni võrrand on järgmine:
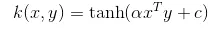
Seda kernelit on tugivektorimasinate seas väga palju kasutatud ja populaarne.
7. Anova radiaalne alusituum - see tuum toimib teadaolevalt väga hästi mitmemõõtmeliste regressiooniprobleemide korral nagu Gaussi ja Laplacia tuum. See kuulub ka radiaalse aluse tuuma kategooriasse.
Anova tuuma võrrand on järgmine:
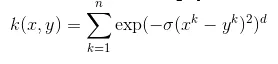
Kernelmeetodeid on palju rohkem ja me oleme arutanud enamkasutatavaid tuumasid. See sõltub puhtalt probleemi tüübist, mis otsustab kasutatava kerneli funktsiooni.
Järeldus
Selles jaotises oleme näinud kerneli määratlust ja selle toimimist. Proovisime diagrammide abil selgitada tuumade tööd. Seejärel oleme proovinud kerneli funktsiooni kohta matemaatikat kasutades lihtsat illustratsiooni anda. Viimases osas oleme näinud erinevat tüüpi kerneli funktsioone, mida tänapäeval laialdaselt kasutatakse.
Soovitatavad artiklid
See on tuumameetodite juhend. Siin käsitleme sissejuhatust, vajadust, selle toimimist ja kerneli meetodite tüüpe koos vastava võrrandiga. Lisateavet leiate ka meie muudest soovitatud artiklitest -
- Andmete kaevandamise algoritmid
- K- tähendab klasterdamisalgoritmi
- Julma jõu algoritm
- Otsustuspuu algoritm
- Tuumameetodid masinõppes
- Otsustuspuu masinõppes