Excel NORMSINV (sisukord)
- Sissejuhatus Excelisse NORMSINV
- Kuidas kasutada NORMSINV valemit Excelis?
Sissejuhatus Excelisse NORMSINV
Normaalse kumulatiivse jaotusfunktsiooni pöördtekst Excelis on oluline tööriist, mis tagastab normaalse kumulatiivse pöördvõrrandi pöördväärtuse antud tõenäosusväärtuse korral, st tavaliselt tagastab tavalise normaalse kumulatiivse jaotuse pöördväärtuse (mille keskmine on null ja standardhälve on üks). Funktsioon NORM.S.INV võetakse esmakordselt kasutusele Microsoft Exceli versioonis 2010, mis on funktsiooni NORMSINV värskendatud versioon versioonis Excel 2013 ja uusim versioon. Funktsiooni NORMSINV kasutatakse enamasti võlgade tasumisel ja finantsanalüüsil.
Exceli NORMSINV süntaks

Argument:
Tõenäosus - mis on kõike muud kui tõenäosus vastab normaaljaotusele.
Kuidas kasutada NORMSINV valemit Excelis?
Microsoft excelis liigitatakse sisseehitatud funktsioon NORMSINV statistilise funktsiooni alla, mis on näidatud alloleval ekraanipildil (kus see arvutab antud tõenäosuse korral normaalse kumulatiivse jaotuse pöördvõrdelisuse).
- Minge menüüsse Valemid.
- Klõpsake nuppu Veel funktsiooni, nagu on näidatud alloleval ekraanipildil.

- Valige statistikakategooria, mille alt leiame funktsiooni NORM.DIST, nagu allpool näidatud.
Näide nr 1 - NORM.DIST ja NORMSINV kasutamine
Funktsiooni NORM.DIST kasutamiseks alustame lihtsast näitest, kus peame välja selgitama õpilaste klassid. Oletame, et meil on klassieksam keskmise hindega 70 st mu = 70 ja klassi standardhälve on 3 punkti ehk sigma = 3 siin peame välja selgitama, kui suur on tõenäosus, et õpilased said hinded 73 või alla selle, st P (X <= 73). Vaatame, kuidas funktsiooni NORM.DIST abil tõenäosust teada saada.
- X = 3
- Keskmine = 70
- Standardhälve = 3
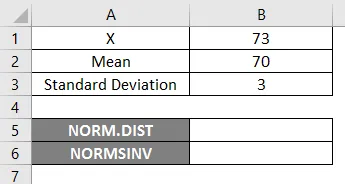
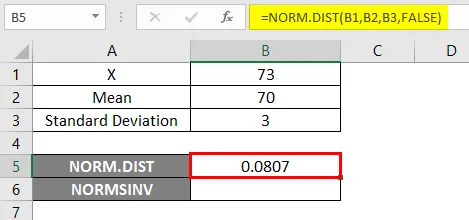
- Rakendage funktsiooni NORM.DIST nagu allpool.
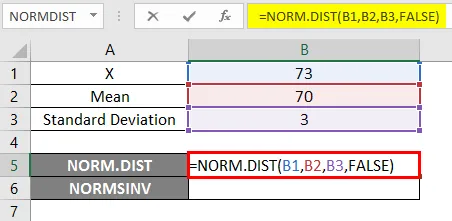
- Kui rakendame ülaltoodud funktsiooni NORM.DIST, saame tõenäosuse 0, 0807.
- Nüüd rakendage funktsiooni NORMSINV, et teada saada allpool toodud normaalse kumulatiivse jaotuse pöördväärtus.
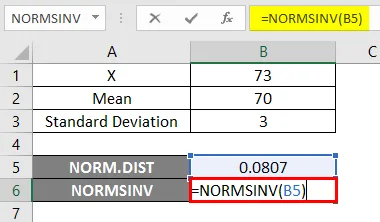
Tulemus -
Allpool toodud tulemuses näeme, et me saime antud tõenäosuse jaoks negatiivsed väärtused -1.40067, st normaalse kumulatiivse jaotuse pöördvõrdeline väärtus.
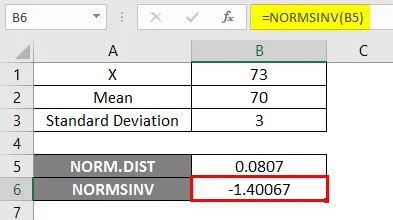
Näide 2 - keskmine ja täpne standardhälve
Vaatame veel ühte näidet kõverapõhiste andmete abil, et saaksime teada keskmist ja täpset standardhälvet.
- Keskmine = 7
- Standardhälve = 1.3
- Standardhälbe suurenemine kui -3

- Helikõvera saamiseks peame lisama standardhälbe juurdekasvule 0, 1, kui andmed on järgmised.
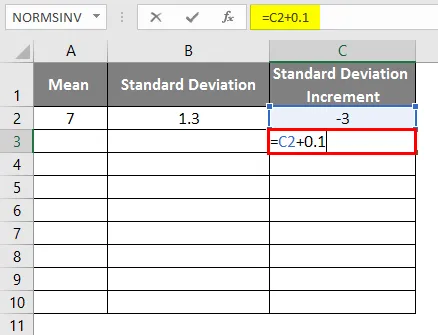
- Pärast valemi rakendamist saadakse järgmine tulemus.
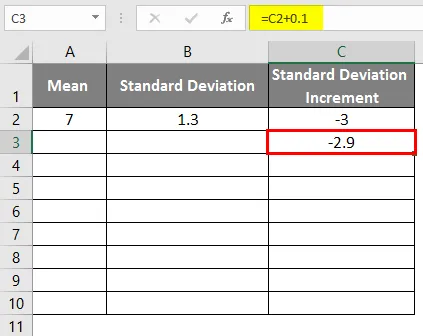
- Lohistage väärtusi, et saada rohkem väärtusi, kuni saame positiivsed väärtused, nii et saame vasaku kõvera.
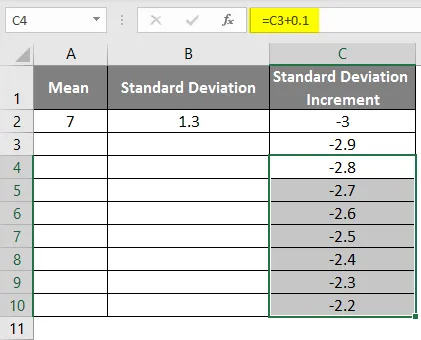
- Parempoolse kõvera saamiseks peame rakendama valemit kui = keskmist standardhälvet * 3, et saada täpsed kõverad.
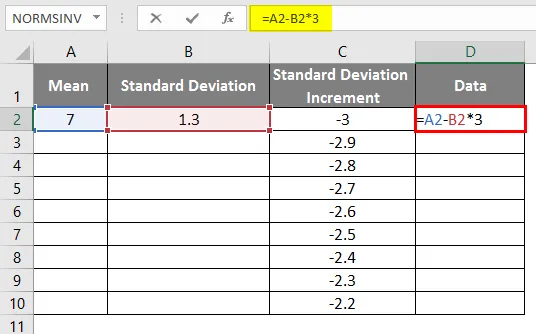
- Pärast valemi kasutamist kuvatakse tulemus allpool.
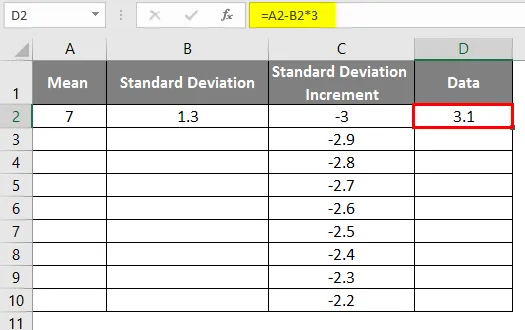
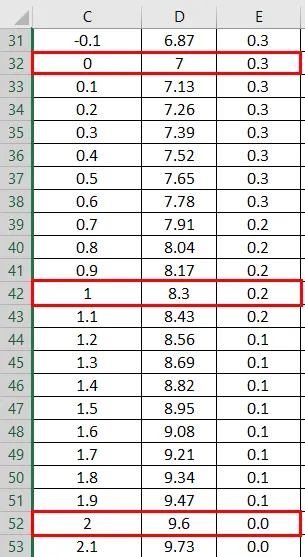
- Nagu ülaltoodud andmetel standardhälbe juurdekasvu jaoks vasaku kõvera saamiseks, oleme väärtusi suurendanud 0, 1 võrra
- Kasutatakse sama stsenaariumi, kasutades valemit = 3.1 + STANDARD DEVIATION / 10, et saada kõvera juurdekasv 0, 1
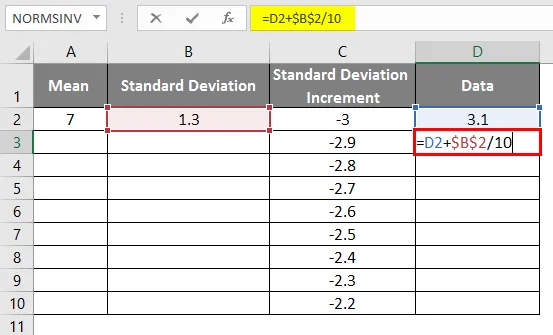
- Pärast valemi kasutamist kuvatakse tulemus allpool.

- Lohistage väärtusi täpse tulemuse saamiseks, mis on näidatud alloleval ekraanipildil.
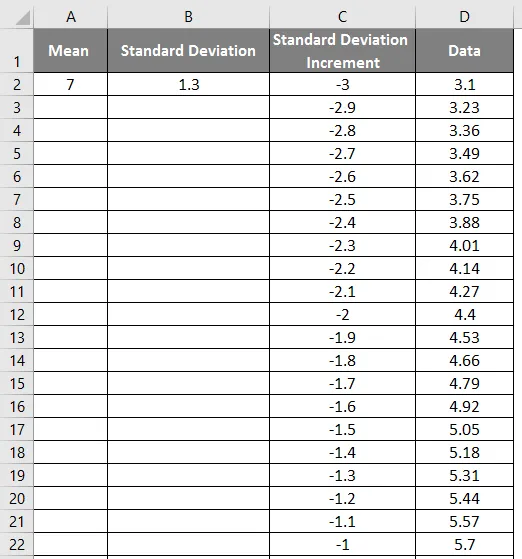
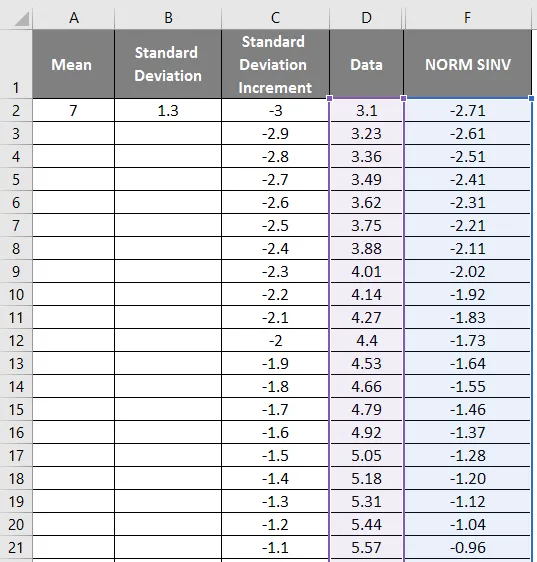
- Nüüd rakendage normaaljaotuse funktsiooni valemiga = NORM.DIST (DATA väärtus, keskmine, standardhälve, vale).
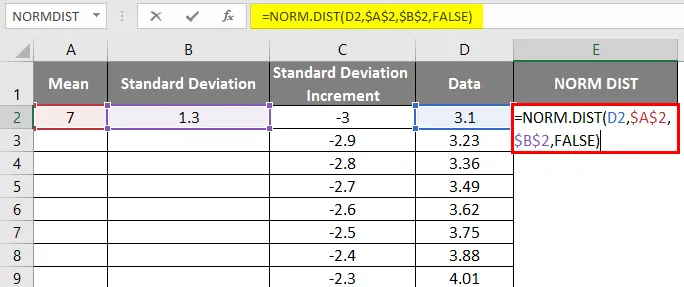
- Allpool toodud tulemuse saame järgmiselt.
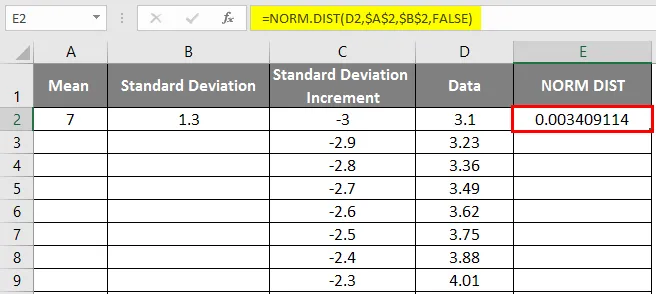
- Allpool näidatud täpse tulemuse saamiseks lohistage väärtusi.
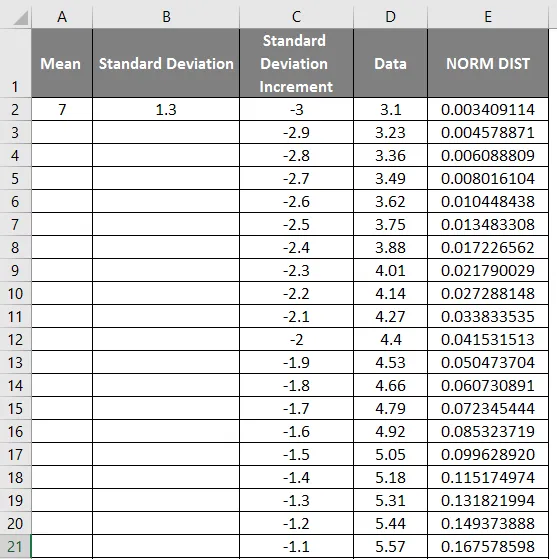
- Nagu ülaltoodud ekraanipildil näeme, oleme keskmise ja standardhälbe põhjal arvutanud NORMAALjaotuse. Nüüd vaatame, milline saab olema NORMAL-i jaotuse pöördvõrde, rakendades allpool näidatud NORMSINV-i.
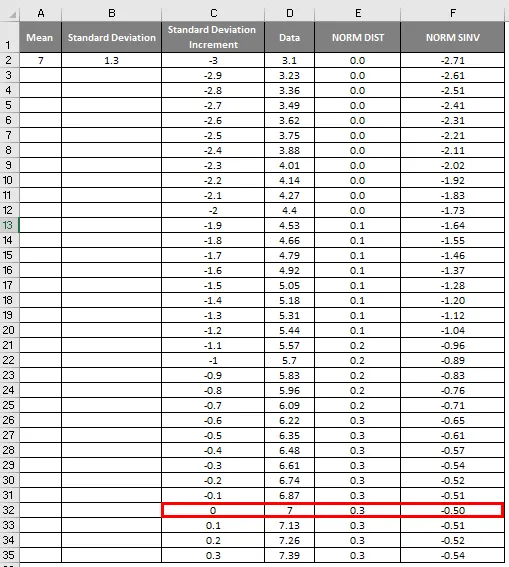
- Siin näeme, et väärtusel Zero (0) on standardhälve 7.

Hajutatud graafiku rakendamine vasaku ja parema kõvera kuvamiseks.
- Kõigepealt valige andmed ja veerg Tavaline.
- Minge vahekaardile Lisa ja valige hajutatud graafik järgmiselt.
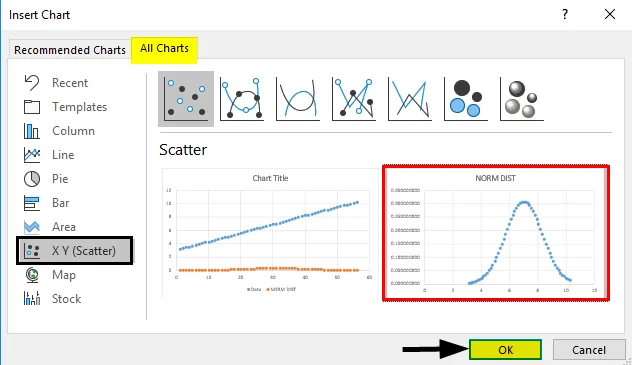
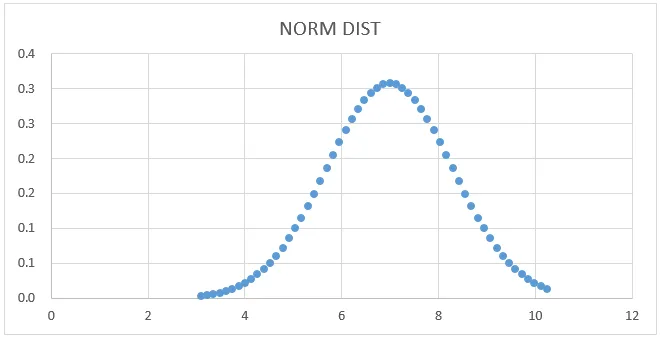
- Saame alloleva kõvera graafiku, nagu allpool näidatud.
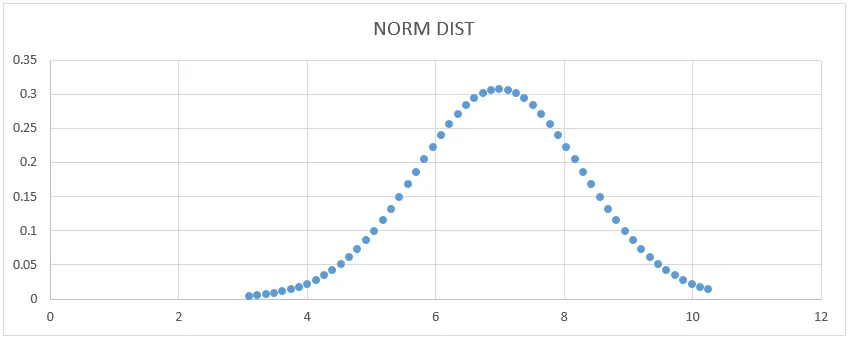
Siin näeme, et keskmisel väärtusel 7 on standardhälbe kuju, mille abil saame seda näidata, joonistades selle sirgjoone.
- Keskmine = 7
- 1 - standardhälve näitab 68% andmetest.
- 2 - standardhälve näitab 95% andmetest.
- 3 - standardhälve näitab 99, 7% andmetest.
Normaalne jaotusgraafik:
NORMSINV graafik:
Valige ülaltoodud jooniselt andmeveerg ja NORM SINV, et saada allpool toodud graafik järgmiselt.
- Kõigepealt valige andmed ja veerg Tavaline.
- Minge vahekaardile Lisa ja valige hajutatud graafik.
- Saame allpool oleva graafiku, mis on näidatud alloleval ekraanipildil.
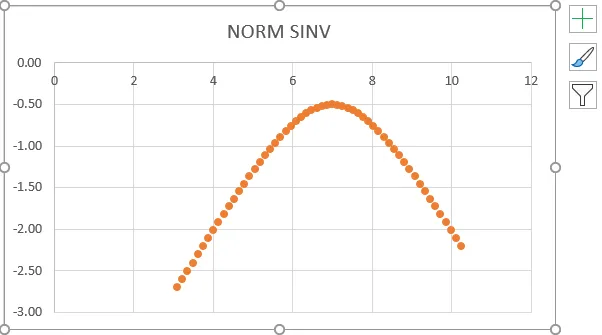
- Ülaltoodud ekraanipildi põhjal näeme, et saime normaaljaotuse täpse pöördvõrrandi, mis näitab sama väärtust, mida on näidatud allpool.

Näide # 3 - vasaku ja parema kõvera seadistamine
Selles näites konfigureerime vasaku ja parema kõvera tavalise jaotusfunktsiooni abil. Mõelge allpool toodud andmetele, kus x-ga on negatiivsed väärtused ja see suurendatakse positiivseteks väärtusteks.
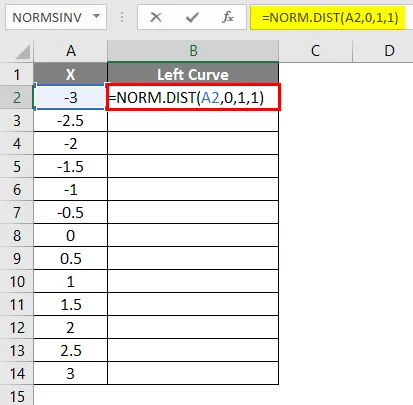
- Rakendage valem = NORM.DIST (A2, 0, 1, 1).
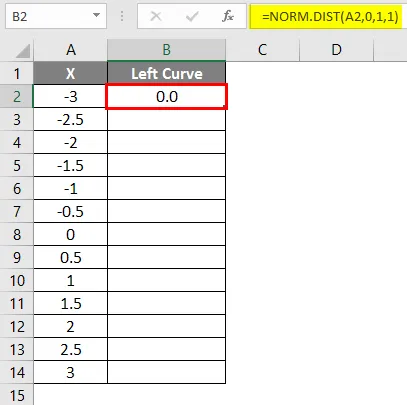
- Pärast valemi rakendamist kuvatakse tulemus allpool.
- Lohistage valem teistes lahtrites.
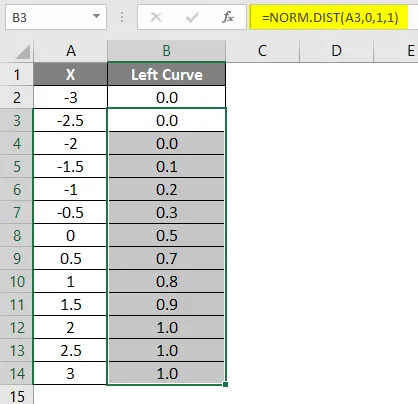
- Rakenda valem = 1-B2 .
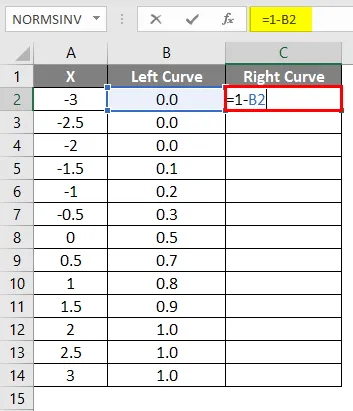
- Pärast valemi rakendamist kuvatakse tulemus allpool.
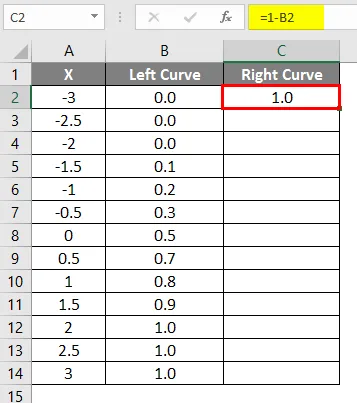
- Lohistage sama valem teistes lahtrites.
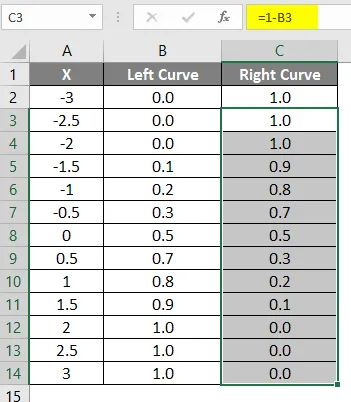
Ülaltoodud valemi tulemus on näidatud allpool.
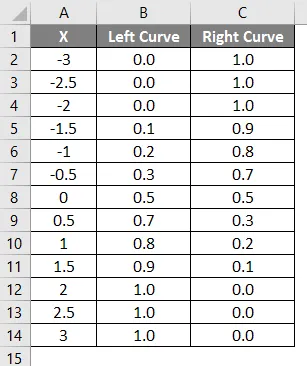
- Vasakpoolse kõvera väärtused on arvutatud NORMAL DISTRIBUTION valemi abil, määrates kumulatiivseks väärtuseks True ja NORMSINV on arvutatud vasakpoolse kõvera abil.
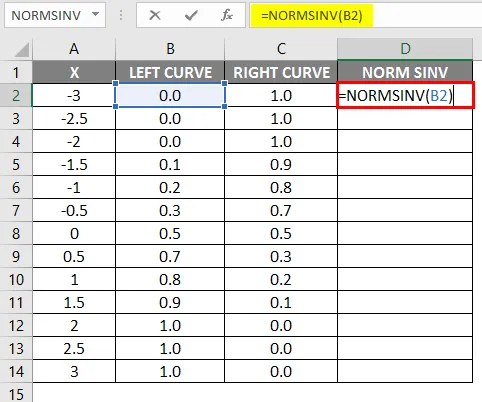
- Pärast valemi rakendamist kuvatakse tulemus allpool.
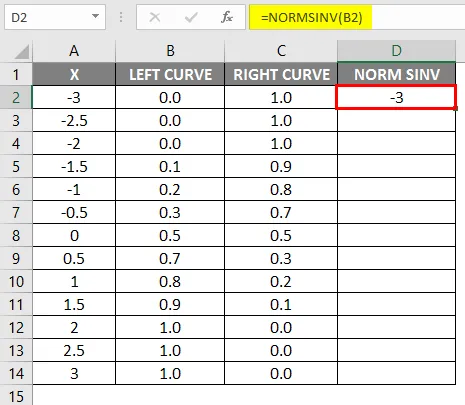
- Lohistage sama valem teistes lahtrites.
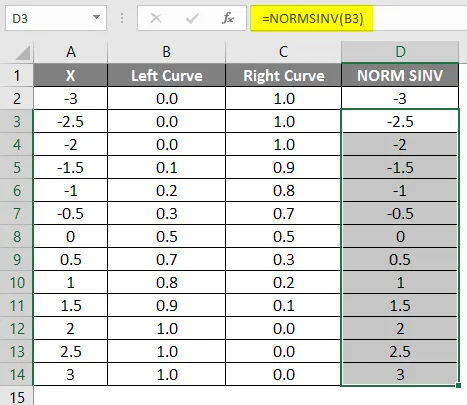
Nagu näeme, et saime NORMSINV jaoks sama väärtuse, mis on midagi muud kui normaaljaotuse pöördvõrdeline väärtus. Samamoodi saame õige kõvera väärtuse, arvutades ühe vasaku kõvera väärtuse. Järgmises etapis kontrollime hajutatud graafiku abil, kuidas saame x-i kõrguse.
- Valige vasak ja parem kõver.
- Minge sisestusmenüüsse.
- Valige hajutatud graafik järgmiselt.
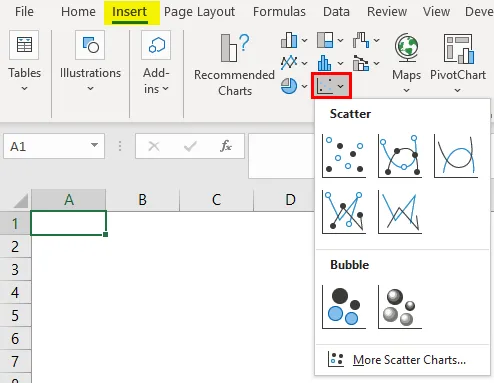
Me saame järgmise graafiku tulemuse, nagu allpool näidatud.
Graafik NORM SINV:
Alloleval graafikul näeme, et väärtuse NORM DISTRIBUTION vasakpoolsel kõveral on täpne vaste (0, 0, 5), mis asub joone keskel, kus saame sama graafiku, kui taotleme NORMDISTi.
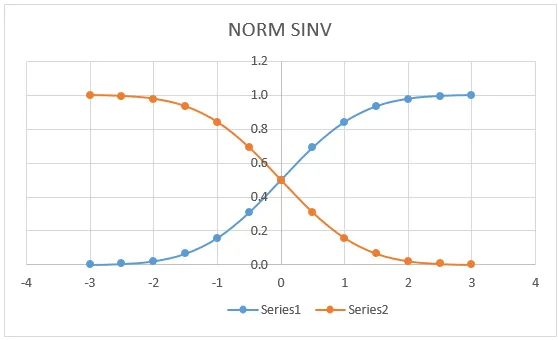
Ülaltoodud graafikul näitab see väga selgelt, et saime täpse keskmise keskpunktis, mis tähistab:
- X = 0
- Vasak kõver = 0, 5
- Parempoolne kõver = 0, 5
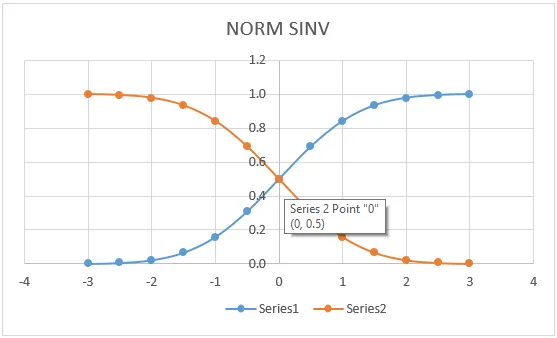
Kuvame selle, et vaadata NORMSINV väärtusi graafilises vormingus, nagu allpool näidatud.
Excel NORMSINV-ist meelde tuletavad asjad
- #väärtus! Viga ilmneb siis, kui antud argument pole arvuline ega loogiline väärtus.
- Funktsioonis Normal Distribution saame tavaliselt #NUM! standardhälbe argumendist tulenev viga on nullist väiksem või sellega võrdne.
Soovitatavad artiklid
See on juhend Excel NORMSINV-i. Siin arutatakse, kuidas kasutada NORMSINV-i Excelis koos praktiliste näidete ja allalaaditava excel-malliga. Võite vaadata ka meie teisi soovitatud artikleid -
- Kuidas nimeboksi Excelis kasutada?
- Töötamine Matrixiga Excelis
- Mis siis, kui analüüs Excelis
- NPV valem Excelis