3D-maatriks MATLAB-is
MATLAB on keel, mida kasutatakse tehniliseks andmetöötluseks. Nagu enamik meist nõustub, on arvutikasutamise, visualiseerimise ja lõpuks programmeerimise ülesannete integreerimiseks vajalik hõlpsasti kasutatav keskkond. MATLAB teeb sama, pakkudes keskkonda, mida pole mitte ainult lihtne kasutada, vaid ka meie pakutavaid lahendusi kuvatakse matemaatiliste märkuste abil, millega enamik meist tuttav on. Selles teemas tutvume 3D-maatriksiga MATLAB-is.
MATLABi kasutusalad hõlmavad
- Arvutamine
- Algoritmide väljatöötamine
- Modelleerimine
- Simulatsioon
- Prototüüpimine
- Andmete analüüs (andmete analüüs ja visualiseerimine)
- Inseneri- ja teadusgraafika
- Rakenduste arendamine
Selles artiklis mõistame MATLAB-i mitmemõõtmelisi massiive ja täpsemalt Matlabis kolmemõõtmelist maatriksit.
Mitmemõõtmeline massiiv
See on MATLAB-i massiiv, millel on kaks või enam mõõdet. Võib-olla te juba teate, et 2D-maatriksi mõõtmeid tähistavad read ja veerud.
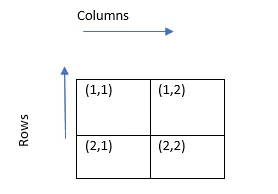
Igal elemendil on kaks alaindeksit - üks on reaindeks ja teine - veeruindeks.
nt (1, 1) element tähistab siin Rida on 1 ja veeru number 1.
Mis on 3D-maatriks?
3-D maatriks on mitmemõõtmeline maatriks, mis on kahemõõtmeliste maatriksite laiendus. Nagu võite arvata, on neil 3 alaindeksit, üks alaindeks koos rea- ja veeruindeksitega nagu kahesuunalise maatriksi puhul. 3D-maatriksi kolmandat alaindeksi kasutatakse elemendi lehtede või lehtede tähistamiseks.
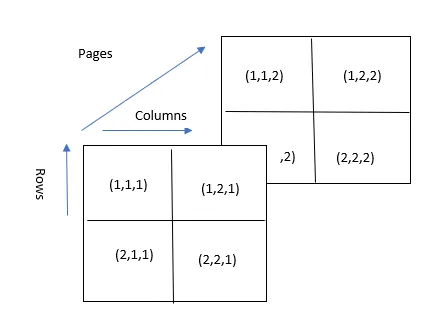
Näiteks siin tähistab element (2, 1, 1) 'Rida' number 2 'Veerg number üks ja' Lehekülg 'number 1.
3D-maatriksi loomine
Saame nüüd aru, kuidas saaksime MATLAB-is luua 3D-maatriksi
3-mõõtmelise massiivi jaoks looge esmalt 2D-maatriks ja laiendage seda siis 3D-maatriksiks.
- Looge kolmemõõtmeline maatriks 3D-massiivi esimese lehena (näete selgelt, et loome kõigepealt 2D-maatriksi)
A = (11 2 7; 4 1 0; 7 1 5)
- Lisage nüüd teine leht. Seda saab teha, määrates veel ühe 3: 3 maatriksi, mille kolmandas dimensioonis on indeksi väärtus 2
A (:, :, 2) = (1 2 5; 4 4 6; 2 8 1)
A (3 × 3)
A =
| A (:, :, 1) = | 11 | 2 | 7 |
| 4 | 1 | 0 | |
| 7 | 1 | 5 |
| A (:, :, 2) = | 1 | 2 | 5 |
| 4 | 4 | 6 | |
| 2 | 8 | 1 |
Mitmemõõtmeliste massiivide loomiseks võime kasutada ka funktsiooni kassi funktsioon.
Näide: looge kassifunktsiooni abil 3-leheküljeline 3D-massiiv
X = kass (3, A, (3 7 1; 0 1 8; 2 5 4))
- Siin A on ülal loodud 3D-massiiv
- Esiteks esitatud argument (3) näitab, millises suunas massiivi tuleb ühendada
- Siin tehakse lehtedega liitmist
X =
| X (:, :, 1) = | 11 | 2 | 7 |
| 4 | 1 | 0 | |
| 7 | 1 | 5 |
| X (:, :, 2) = | 1 | 2 | 3 |
| 4 | 4 | 6 | |
| 2 | 8 | 1 |
| X (:, :, 3) = | 3 | 7 | 1 |
| 0 | 1 | 8 | |
| 2 | 5 | 4 |
Nüüd, kui me peame seda massiivi veelgi laiendama, saame lihtsalt anda 4. massiivi elemendid, mida peame lisama:
Ülaltoodud näite laiendamiseks anname lihtsalt,
B (:, :, 4) = (1 2 1; 3 9 1; 6 3 7) ja väljund on:
X =
| X (:, :, 1) = | 11 | 2 | 7 |
| 4 | 1 | 0 | |
| 7 | 1 | 5 |
| X (:, :, 2) = | 1 | 2 | 3 |
| 4 | 4 | 6 | |
| 2 | 8 | 1 |
| X (:, :, 3) = | 3 | 7 | 1 |
| 0 | 1 | 8 | |
| 2 | 5 | 4 |
| X (:, :, 4) = | 1 | 2 | 1 |
| 3 | 9 | 1 | |
| 6 | 3 | 7 |
Kuidas pääseme juurde massiivi elementidele?
Selleks kasutage lihtsalt alaindereid täisarvudena. Niisiis, 3D-maatriksi 2, 3, 1 element on element, mis asub 1. lehe 2. reas, 3. veerus
Kasutame selle demonstreerimiseks 3D-maatriksit A, mida kasutasime ülal,
Nüüd annab juurdepääs = A (2, 3, 1) meile väljundina 0
Mitmemõõtmelise massiivi elementidega manipuleerimise funktsioonid
MATLAB pakub meile paar funktsiooni, et manipuleerida mitmemõõtmelise massiivi elementidega.
- Muutke ümber
- Permute
Saame neist aru ükshaaval:
1. Muutke ümber
See on kasulik peamiselt andmete visualiseerimise ajal
Näide: looge kahe 3 * 5 maatriksi abil 6 * 5 maatriks
- A = (1 3 7 0 5; 2 0 4 1 3; 1 0 5 3 2);
- A (:, :, 2) = (1 7 2 5 0; 4 2 1 6 5; 1 1 4 5 0);
- B = ümberkujundamine (A, (6 5))
See loob 2D maatriksi, milles on 6 rida ja 5 veergu:
B = 6 × 5
1 7 5 7 5
2 4 3 2 6
1 5 2 1 5
3 0 1 2 0
0 1 4 1 5
0 3 1 4 0
Nagu võite märgata, töötab RESHAPE veergude kaupa, nii et kõigepealt võta A kõik elemendid esimese lehe jaoks veerust. Sama asi tehakse siis ka 2. lehe jaoks
2. Permute
Saame seda funktsiooni kasutada, kui tahame maatriksite mõõtmeid ümber korraldada. st ridade vahetamine veergudega või vastupidi.
Permuti näide
- P (:, :, 1) = (3 5 3; 1 5 2; 0 8 5);
- P (:, :, 2) = (0 1 3; 6 7 1; 4 2 1)
Kasutagem nüüd funktsiooni PERMUTE P-s:
- M = permute (P, (2 1 3))
Saadaval väljundil vahetatakse read ja veerud järgmiselt:
M1 =
| M1 (:, :, 1) = | 3 | 1 | 0 |
| 5 | 5 | 8 | |
| 3 | 2 | 5 |
| P1 (:, :, 2) = | 0 | 6 | 4 |
| 1 | 7 | 2 | |
| 3 | 1 | 1 |
Soovitatavad artiklid
See on MATLAB-i 3D-maatriksi juhend. Siin käsitleme MATLABi kasutamist, mis on 3 D maatriks? ja kuidas luua MATLAB-is 3D-massiive ja nendega ka mõningaid manipulatsioone. Lisateabe saamiseks võite vaadata ka järgmist artiklit -
- Maatriks Matlabis
- MATLABi versioon
- Vektorid Matlabis
- Andmetüübid MATLAB-is
- Taru andmete tüüp
- PL / SQL andmetüübid