
F-testi valem (sisukord)
- Valem
- Näited
Mis on F-testi valem?
F-test on statistiline test, mis aitab meil välja selgitada, kas kahel populatsioonikomplektil, millel on nende andmepunktide normaalne jaotus, on sama standardhälve või dispersioon. Kuid esimene ja peamine asi, mida F-testi jaoks teha, on see, et andmekogumitel peaks olema normaalne jaotus. Seda rakendatakse F-jaotusele nullhüpoteesi korral. F-test on dispersioonanalüüsi (ANOVA) väga oluline osa ja selle arvutamiseks võetakse kahe erineva andmekogumi kahe variatsiooni suhted. Kuna me teame, et dispersioonid annavad meile teavet andmepunktide hajutamise kohta. F-testi kasutatakse ka erinevates testides nagu regressioonanalüüs, Chow-test jne.
F-testi valem:
F-testi jaoks pole lihtsat valemit, kuid see on rida toiminguid, mida peame järgima:
1. samm: F-testi tegemiseks peame kõigepealt määratlema nullhüpoteesi ja alternatiivse hüpoteesi. Need on andnud:
- H0 (nullhüpotees): 1. andmekogumi dispersioon = teise andmekogumi dispersioon
- Ha: 1. andmekogumi dispersioon <2. andmestiku dispersioon (madalama ühepoolse katse jaoks)
- Ha: 1. andmekogumi dispersioon> teise andmekogumi variatsioon (ülemise ühepoolse katse jaoks)
- Ha: 1. andmekogumi dispersioon ≠ 2. andmekogu variatsioon (kahepoolse katse jaoks)
2. samm: Järgmine asi, mida peame tegema, on see, et peame välja selgitama olulisuse taseme ja seejärel määrama nii lugeja kui ka nimetaja vabadusastmed. See aitab meil nende kriitilisi väärtusi kindlaks määrata. Vabadusaste on proovi suurus -1.
3. samm: F-testi valem:
F Value = Variance of 1 st Data Set / Variance of 2 nd Data Set
4. samm: leidke tabelist F kriitiline väärtus, võttes arvesse vabaduse ja olulisuse astet.
5. samm: võrrelge neid kahte väärtust ja kui kriitiline väärtus on väiksem kui F väärtus, võite nullhüpoteesi tagasi lükata.
F-testi valemi näited (Exceli malliga)
Võtame näite, et mõista paremini F-testi arvutamist.
Selle F-TEST Formula Exceli malli saate alla laadida siit - F-TEST Formula Exceli mallF-testi valem - näide # 1
Oletame, et meil on kaks andmekogumit A ja B, mis sisaldavad erinevaid andmepunkte. Tehke F-test, et teha kindlaks, kas me võime nullihüpoteesi tagasi lükata 1% olulisuse tasemel.
Andmekogumid:
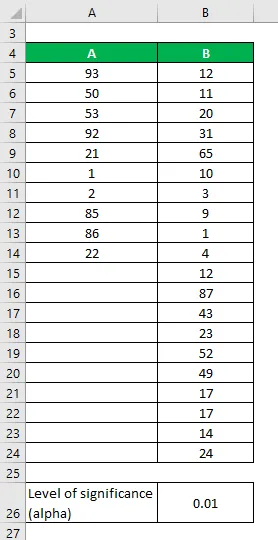
Lahendus:
Nullhüpotees: A variatsioon = B variatsioon
Vabadusaste arvutatakse järgmiselt:
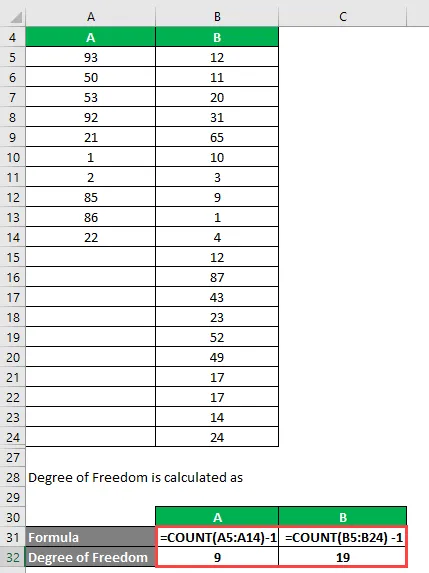
Vabadusaste
- A = 10 - 1 = 9 korral
- Kui B = 20 - 1 = 19
Variatsioon arvutatakse järgmiselt:

- Variatsioon A = 1385, 61
- Variatsioon B = 521, 22
F väärtus arvutatakse järgmise valemi abil
F väärtus = esimese andmekogumi variatsioon / teise andmekogu variatsioon
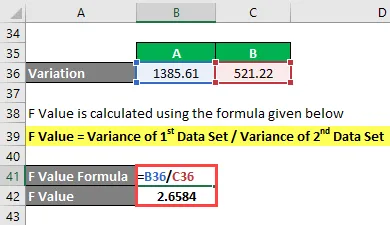
- F väärtus = 1385, 61 / 521, 22
- F väärtus = 2, 6584
F-tabel:
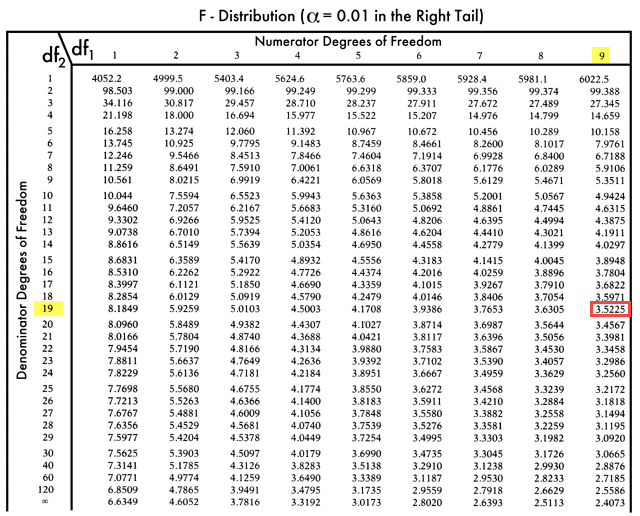
Nii et F kriitiline väärtus = 3, 5225
Kuna F kriitiline on suurem kui F väärtus, ei saa nullihüpoteesi tagasi lükata.
F-testi valem - näide # 2
Oletame, et töötate teadusettevõttes ja soovite teada, kui suur on süsinikoksiidi emissiooni tase 2 erinevat marki sigarette ja kas need on oluliselt erinevad või mitte. Oma analüüsis olete kogunud järgmise teabe:
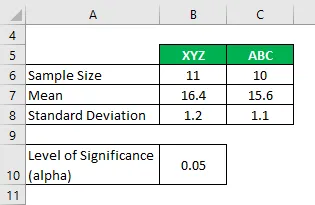
Lahendus:
Vabadusaste arvutatakse järgmiselt:
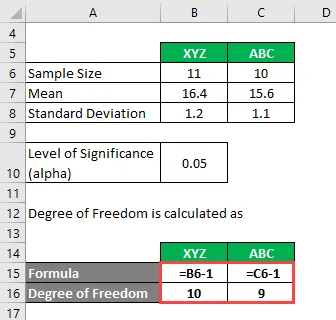
Vabadusaste
- XYZ = 11 - 1 = 10 korral
- Kui ABC = 10 - 1 = 9
Variatsioon arvutatakse järgmiselt:
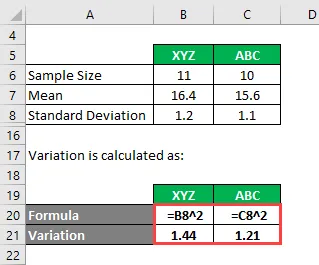
- XYZ dispersioon = 1, 2 2 = 1, 44
- ABC dispersioon = 1, 1 2 = 1, 21
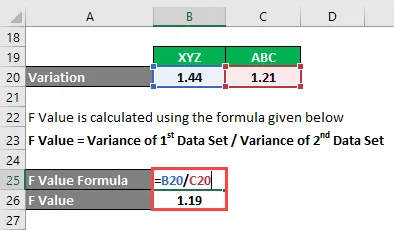
- F väärtus = 1, 44 / 1, 21
- F väärtus = 1, 19
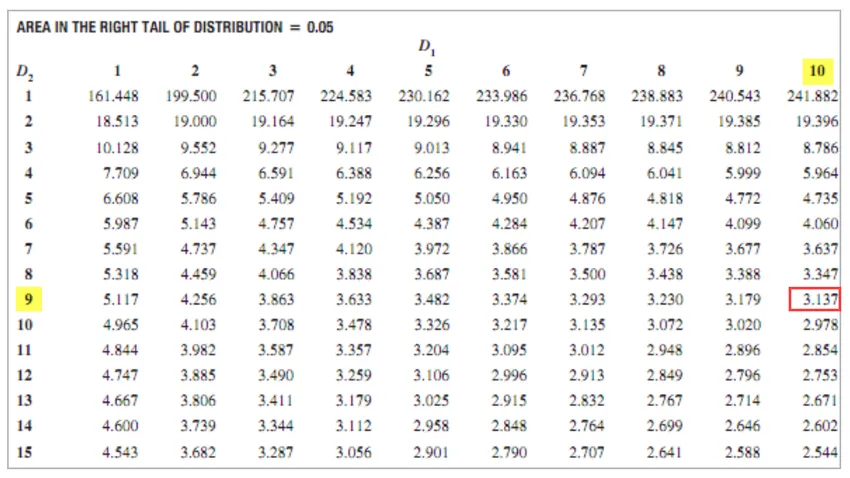
F Kriitiline väärtus = 3, 137
Kuna väärtus F on kriitiline> F, ei saa nullhüpoteesi tagasi lükata.
Seletus
Ülaltoodud näidetes nägime F-testi rakendamist ja selle toimimist. Kuid on olemas eeldus, mille peame enne F-testi läbiviimist hoolikalt jälgima, vastasel juhul ei saa me nõutavaid tulemusi:
- Esimene asi on see, et F-väärtuse arvutamisel peame alati paigutama kõrgema dispersiooniväärtuse lugeja. Seega, kui F = V1 / V2, peaks V1 olema> V2
- Kui tahame läbi viia 2 sabatesti, peame olulisuse taseme jagama kahega ja see on kriitilise väärtuse leidmiseks õige tase
- F-väärtuse arvutamisel kasutame ainult dispersiooni ja kui meile antakse standardhälbed, nagu näites 2, peavad need dispersiooni leidmiseks olema ruudus.
- Mõlemad valimid peaksid olema üksteisest sõltumatud ja valimi suurus peaks olema alla 30 mm
- Valikukogumid, millest proovid võetakse, peavad tavaliselt jaotuma
Need on peamised parameetrid / eeldus, mille eest tuleks F-testi tegemise ajal hoolitseda.
F-testi valemi asjakohasus ja kasutamine
Nagu eespool arutatud, aitab F-test meil kontrollida kahe populatsiooni variatsiooni võrdsust. Nii et kui meil on kaks sõltumatut valimit, mis on võetud tavalisest populatsioonist ja tahame kontrollida, kas neil on sama varieeruvus või mitte, kasutame F-testi. F-testil on suur tähtsus ka regressioonanalüüsis ja ka R2 olulisuse testimisel. Lühidalt öeldes on F-Test statistikas väga oluline tööriist, kui soovime võrrelda kahe või enama andmekogumi variatsiooni. Kuid enne selle testi tegemist tuleks kõiki eeldusi meeles pidada.
Soovitatavad artiklid
See on olnud F-testi valemi juhend. Siin arutatakse, kuidas arvutada F-test koos praktiliste näidete ja allalaaditava Exceli malliga. Lisateabe saamiseks võite vaadata ka järgmisi artikleid -
- T jaotuse valem
- Võlakirjade hinnakujunduse valem
- Vormi protsent
- NOPAT-i valemi arvutamine