Lineaarne regressioon Excelis - Kuidas teha lineaarset regressiooni Excelis?

Lineaarne regressioon Excelis (sisukord)

Sissejuhatus lineaarsesse regressiooni Excelis
Lineaarse regressiooni kasutamise meetodid Excelis

Sissejuhatus lineaarsesse regressiooni Excelis

Lineaarne regressioon on statistiline tehnika / meetod, mida kasutatakse kahe pideva kvantitatiivse muutuja vahelise seose uurimiseks. Selles tehnikas kasutatakse sõltuva muutuja väärtuse ennustamiseks sõltumatuid muutujaid. Kui on ainult üks sõltumatu muutuja, siis on see lihtne lineaarne regressioon ja kui mitu sõltumatut muutujat on rohkem kui üks, siis on tegemist mitme lineaarse regressiooniga. Lineaarse regressiooni mudelitel on seos sõltuvate ja sõltumatute muutujate vahel, sobitades vaadeldavatele andmetele lineaarse võrrandi. Lineaarne viitab asjaolule, et me kasutame rida oma andmete sobitamiseks. Regressioonanalüüsis kasutatavaid sõltuvaid muutujaid nimetatakse ka reageerimise või ennustatud muutujateks ning sõltumatuid muutujaid nimetatakse ka seletavateks muutujateks või ennustajateks.

Lineaarsel regressioonisirgel on selline võrrand: Y = a + bX;

Kus:

X on selgitav muutuja,
Y on sõltuv muutuja,
b on joone kalle,
a on y-ristlõige (st y väärtus, kui x = 0).

Väikseimate ruutude meetodit kasutatakse tavaliselt lineaarses regressioonis, mille abil arvutatakse vaadeldud andmete jaoks kõige sobivam joon, minimeerides andmepunktide joonest kõrvalekaldumise ruutude summa.

Lineaarse regressiooni kasutamise meetodid Excelis

Selles näites õpetatakse teile meetodeid Lineaarse regressiooni analüüsi tegemiseks Excelis. Vaatame mõnda meetodit.

Selle lineaarse regressiooni Exceli malli saate alla laadida siit - Lineaarse regressiooni Exceli mall

Meetod nr 1 - hajumisdiagramm trendijoonega

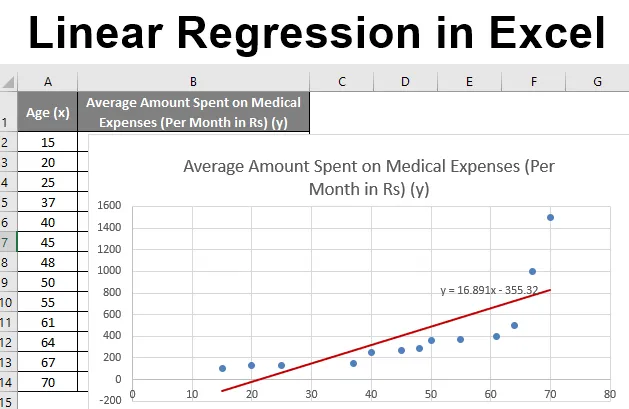
Ütleme nii, et meil on mõnede inimeste andmekogum nende vanuse, bio-massiindeksi (KMI) ja summaga, mille nad kuus ravikuludeks kulutavad. Nüüd soovime ülevaate üksikisikute omadustest, nagu vanus ja KMI, teada saada, kuidas need muutujad mõjutavad ravikulusid, ja kasutada neid regressiooni teostamiseks ning mõne konkreetse inimese keskmiste ravikulude prognoosimiseks / prognoosimiseks. Vaatame kõigepealt, kuidas ainult vanus mõjutab ravikulusid. Vaatame andmekogumit:

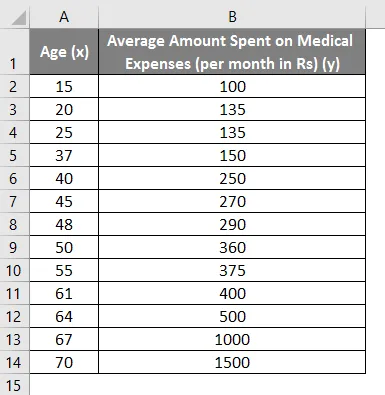
Ravikulude summa = b * vanus + a

Valige andmekogumi kaks veergu (x ja y), sealhulgas päised.

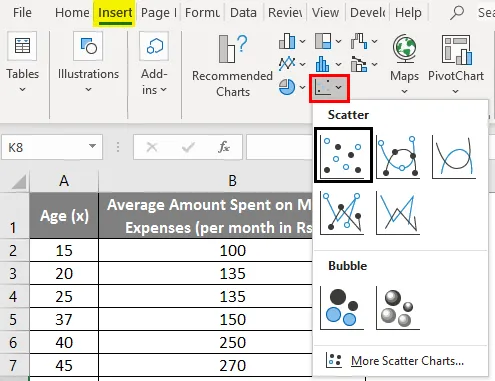
Klõpsake nuppu "Lisa" ja laiendage rippmenüüd "hajumiskaart" ja valige "hajumise" pisipilt (esimene)

Nüüd ilmub hajutatud graafik ja sellele tõmbaksime regressioonijoone. Selleks paremklõpsake mis tahes andmepunkti ja valige 'Lisa trendisuund'

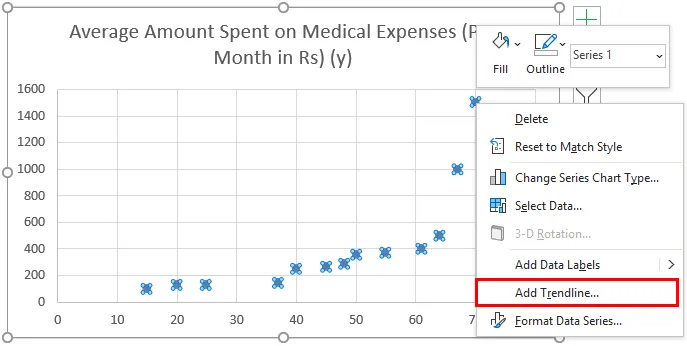
Valige parempoolsel paanil „Format Trendline” suvandid „Linear Trendline” ja „Display Equation on Chart”.

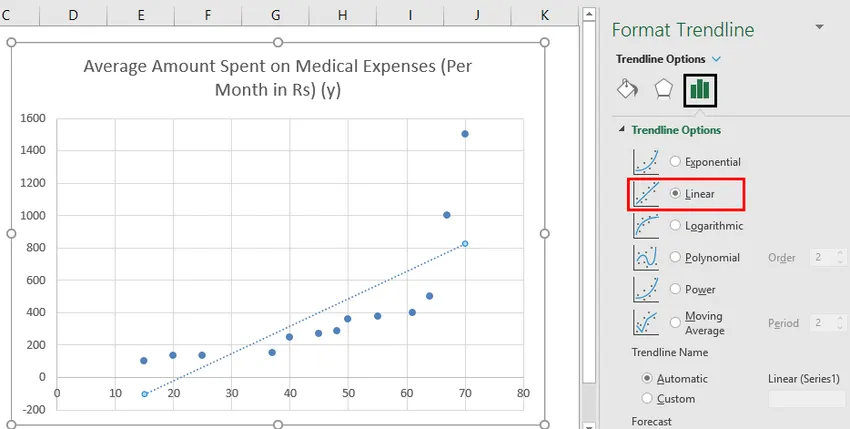
Valige 'Kuva võrrand diagrammil'.

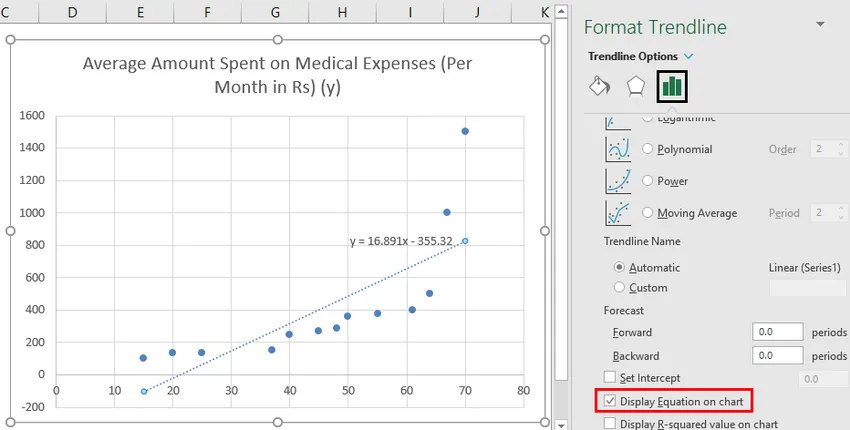
Saame diagrammi vastavalt oma nõudmistele improviseerida, näiteks lisada telgede pealkirju, muuta skaalat, värvi ja joone tüüpi.

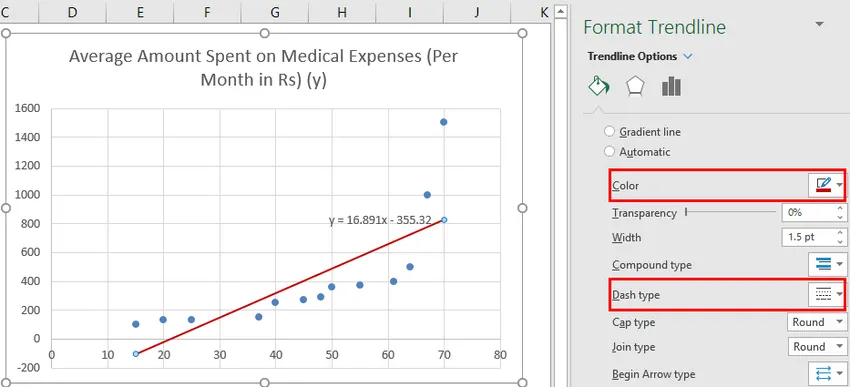
Pärast diagrammi parendamist on see väljund, mille saame.

Märkus . Seda tüüpi regressioonigraafiku korral peaks sõltuv muutuja olema alati y-teljel ja x-teljel sõltumatu. Kui graafik joonistatakse vastupidises järjekorras, siis vahetage teljed diagrammis või vahetage veerud andmestikus.

Meetod nr 2 - analüüsi tööriistapaki lisandmooduli meetod

Analysis ToolPak pole mõnikord vaikimisi lubatud ja me peame seda tegema käsitsi. Selleks tehke järgmist.

Klõpsake menüüd 'Fail'.

Pärast seda klõpsake nuppu "Valikud".

Valige väljast „Halda” „Exceli lisandmoodulid” ja klõpsake nuppu „Mine”

Valige 'Analysis ToolPak' -> 'OK'

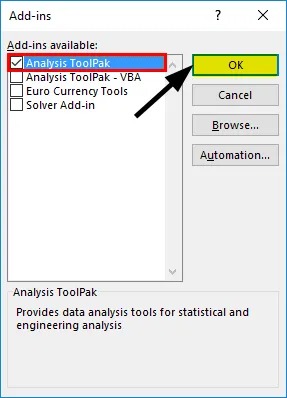
See lisab vahekaardile Andmed andmeandmete analüüsi tööriistad. Nüüd teostame regressioonanalüüsi:

Klõpsake vahekaardi "Andmed" nuppu "Andmete analüüs"

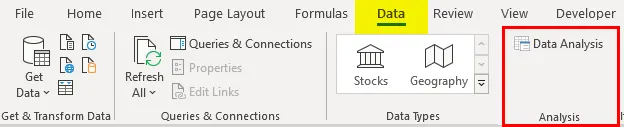
Valige 'Regressioon' -> 'OK'

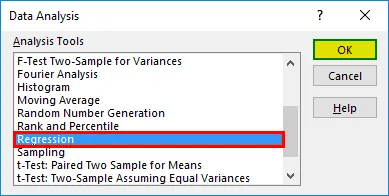
Ilmub regressioonidialoog. Valige sisendi Y vahemik ja sisendi X vahemik (vastavalt ravikulud ja vanus). Mitme lineaarse regressiooni korral saame valida rohkem sõltumatute muutujate veerge (näiteks kui soovime näha ka KMI mõju ravikuludele).
Päiste lisamiseks märkige ruut Sildid.
Valige soovitud väljund.
Valige märkeruut 'jäägid' ja klõpsake nuppu 'OK'.

Nüüd luuakse meie regressioonianalüüsi väljund uuel töölehel, kus on kirjas regressioonistatistika, ANOVA, jäägid ja koefitsiendid.

Väljundi tõlgendamine:

Regressioonistatistika näitab, kui hästi regressioonivõrrand andmetele sobib:

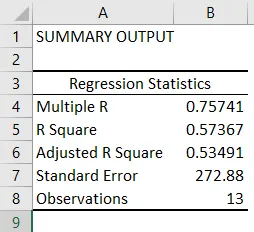
Mitu R on korrelatsioonikordaja, mis mõõdab kahe muutuja vahelise lineaarse suhte tugevust. See jääb vahemikku -1 ja 1 ning selle absoluutväärtus kujutab seose tugevust suure väärtusega, mis näitab tugevamat seost, madal väärtus näitab negatiivset ja nullväärtus näitab, et suhet pole.
R-ruut on määramiskoefitsient, mida kasutatakse sobivuse näitajana. See jääb vahemikku 0–1 ja väärtus lähedane 1 näitab, et mudel sobib hästi. Sel juhul on 0, 57 = 57% y-väärtustest seletatav x-väärtustega.
Reguleeritud R-ruut on R-ruut, mida kohandatakse ennustajate arvu järgi mitme lineaarse regressiooni korral.
Standardviga kujutab regressioonanalüüsi täpsust.
Vaatlused kujutavad mudelvaatluste arvu.
Anova kirjeldab regressioonimudeli varieeruvuse taset.

Seda ei kasutata tavaliselt lihtsa lineaarse regressiooni jaoks. F-olulisuse väärtused näitavad aga, kui usaldusväärsed on meie tulemused, mille väärtus üle 0, 05 soovitab valida mõne muu ennustaja.

Koefitsiendid on regressioonivõrrandi koostamisel kõige olulisem osa.

Meie regressioonivõrrand oleks järgmine: y = 16, 891 x - 355, 32. See on sama, mis 1. meetodil (trendijoonega hajutatud diagramm).

Kui me soovime prognoosida keskmisi ravikulusid, kui vanus on 72 aastat:

Niisiis, y = 16, 891 * 72 -355, 32 = 860, 832

Nii saame ennustada y väärtusi kõigi teiste x väärtuste korral.

Jäägid näitavad tegelike ja ennustatud väärtuste erinevust.

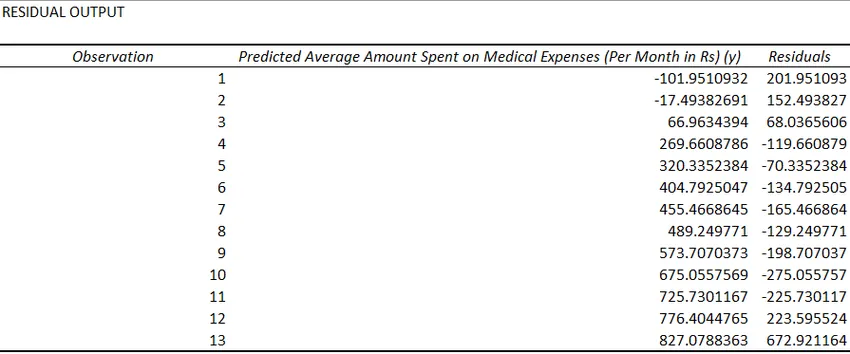
Viimast regressioonimeetodit ei kasutata nii sageli ja regressioonianalüüsi tegemiseks on vaja selliseid statistilisi funktsioone nagu kalle (), vahelejätmine (), korrel () jne.

Lineaarse regressiooni meeldejätmine Excelis

Regressioonanalüüsi kasutatakse tavaliselt selleks, et näha, kas kahe muutujakomplekti vahel on statistiliselt oluline seos.
Seda kasutatakse sõltuva muutuja väärtuse ennustamiseks ühe või mitme sõltumatu muutuja väärtuste põhjal.
Kui soovime lineaarse regressioonimudeli sobitada andmerühmaga, tuleb andmete vahemikku hoolikalt jälgida, nagu kasutaksime regressioonivõrrandit mis tahes väärtuse prognoosimiseks väljaspool seda vahemikku (ekstrapoleerimine), siis võib see põhjustada valesid tulemusi.

Soovitatavad artiklid

See on Exceli lineaarse regressiooni juhend. Siin arutatakse, kuidas teha Lineaarset regressiooni Excelis koos praktiliste näidete ja allalaaditava excelimalliga. Võite vaadata ka meie teisi soovitatud artikleid -