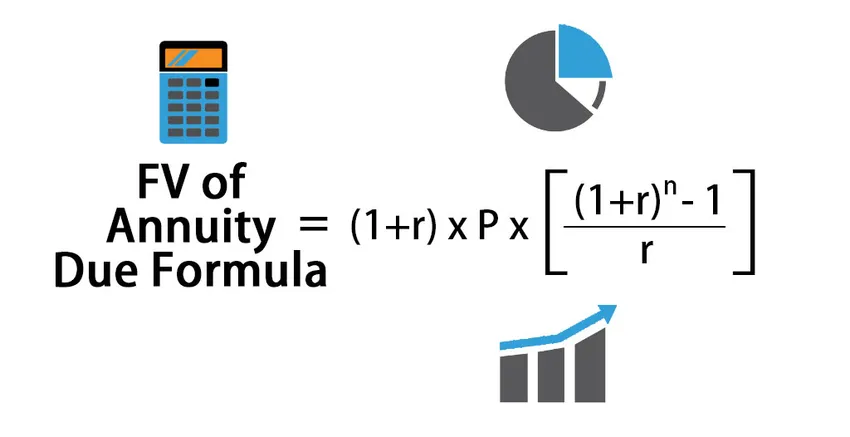
Annuiteedivormi tulevikväärtus (sisukord)
- Annuiteedivormi tulevane väärtus
- Näited annuiteedivormi tulevikväärtusest (Exceli malliga)
- Annuiteedivormi kalkulaatori tulevikuväärtus
Annuiteedivormi tulevane väärtus
Maksmisele kuuluva annuiteedi tulevase väärtuse arvutamise valem:
FV of Annuity Due = (1+r) * P * (((1+r) n – 1) / r )
Kus,
- P = perioodiline makse
- R = määr perioodi kohta
- N = perioodide arv
Näited annuiteedivormi tulevikväärtusest (Exceli malliga)
Võtame näite, et paremini mõista annuiteedi tulevikuväärtuse arvutamist.
Selle annuiteedivormi Exceli tulevase väärtuse tulevikuväärtuse saate alla laadida siit - Vormel Exceli annuiteedi tulevikuväärtusNäide nr 1
Oletame, et Anand on deponeerinud aastas 10 000 dollarit ja tema konto pakutav efektiivne intressimäär on 3%. Nüüd soovib Anand arvutada oma tulevase bilansi 5 aasta pärast, võttes tänasest esimese sissemakse.
Lahendus:
Makstava annuiteedi tulevikuväärtus arvutatakse järgmise valemi abil
Tähtaegse annuiteedi FV = (1 + r) * P * (((1 + r) n - 1) / r)
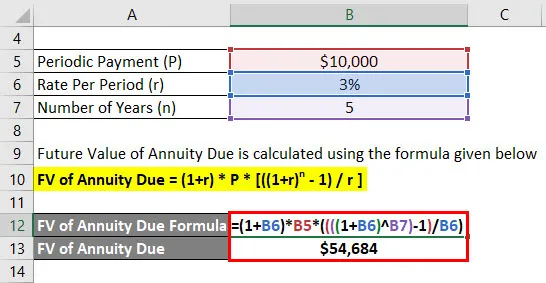
- Tähtpäevaks makstav FV = (1+ 3%) * 10 000 USD * (((((1 + 3%) 5) - 1) / 3%)
- FV makstava annuiteedi eest = 54 684 dollarit
Anand saab 5 aasta pärast tulevikus 54 684 dollarit.
Näide 2
Oletame, et Jagriti on deponeerinud aastas 8000 dollarit ja tema konto pakutav efektiivne intressimäär on 5%. Nüüd soovib Jagriti arvutada oma tulevase saldo 5 aasta pärast, võttes tänasest esimese sissemakse.

Lahendus:
Makstava annuiteedi tulevikuväärtus arvutatakse järgmise valemi abil
Tähtaegse annuiteedi FV = (1 + r) * P * (((1 + r) n - 1) / r)
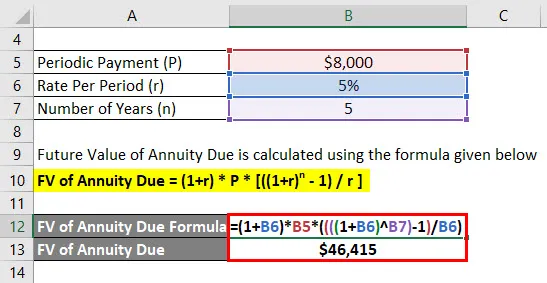
- Tähtpäevaks makstav FV = (1+ 5%) * 8000 USD * (((((1 + 5%) 5) - 1) / 5%)
- FV makstava annuiteedi eest = 46 415 dollarit
Jagriti saab 5 aasta pärast tulevikus 46 415 dollarit.
Näide 3
Oletame, et Anandriti on hoiustanud 20 000 dollarit aastas ja tegelik intressimäär, mida tema konto pakub, on 2%. Nüüd soovib Anandriti arvutada oma tulevase saldo 5 aasta pärast, võttes tänasest esimese sissemakse.
Lahendus:
Makstava annuiteedi tulevikuväärtus arvutatakse järgmise valemi abil
Tähtaegse annuiteedi FV = (1 + r) * P * (((1 + r) n - 1) / r)
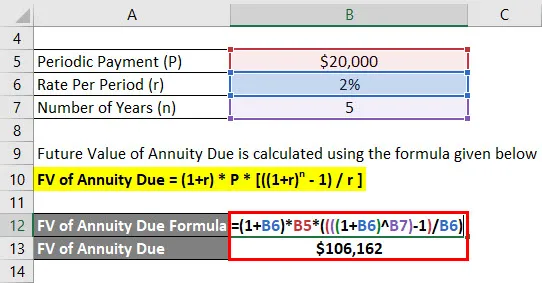
- FV makstava annuiteedi korral = (1+ 2%) * 20 000 USD * (((((1 + 2%) 5) - 1) / 2%)
- FV makstava annuiteedi eest = 1 066 162 dollarit
Anandriti saab 5 aasta pärast 1 066 162 dollari suuruse tulevase saldo.
Seletus
Rahavoogude või maksete rea lõpparvu arvutamiseks, kui esimene osamakse laekub kohe, kasutame makstava annuiteedi tulevikuväärtust. Esimene kohene sissemakse või makse eristab annuiteeti tavalise annuiteedi tõttu. Kohest või kohest annuiteeti nimetatakse makstavaks annuiteediks.
See arvutab rahavoogude väärtuse tulevasel perioodil. Makstava annuiteedi FV kasutamine erineb tegelikes olukordades makstava annuiteedi nüüdisväärtusest. Oletame näiteks, et ettevõte või üksikisik ostab annuiteedi ja on täna esimese osamakse tasunud. Saame näite abil täiendavalt selgitada, oletame, et ettevõte või üksikisik soovib kelleltki annuiteeti osta ja on täna juba esimese makse teinud. Selles olukorras makstava hinna arvutamiseks võime kasutada annuiteedi nüüdisväärtuse valemit. Kui aga soovime arvutada järelejäänud saldo pärast 5-aastase kontole intressi salvestamist ja otsustasime esimese osamakse tasuda täna, kasutatakse sel juhul annuiteedi tulevast väärtust. Makstavat annuiteeti saab selgitada annuiteediliigina, mille rahavood tekivad iga perioodi alguses. Rahavoogude arenenud iseloomu tõttu tuleb iga rahavoogude puhul kohaldada liitmõju igal lisaperioodil, kui seda võrreldakse tavalise annuiteediga. Tavalise annuiteedi tulevikuväärtus on madalam kui annuiteedi tulevikuväärtus, kuna annuiteedi tulevase väärtuse suhtes võetakse perioodiliselt vastu üks tegur.
Tähtaegse annuiteedi tulevikuväärtuse olulisus ja kasutamine
Saame aru tulevase väärtuse ja annuiteedi tähendusest eraldi. Tuleviku väärtust saab selgitada kui sularahasumma koguväärtust, mis tuleb tulevikus maksta konkreetsel kuupäeval. Ja makstavat annuiteeti saab selgitada maksete seeriana, mis tehakse iga perioodi alguses korrapäraselt. Seetõttu saab makstava annuiteedi tulevase väärtuse seletada koguväärtusena tulevikus kindlal kuupäeval süsteemsete / perioodiliste maksete seerias, kus maksed tehakse iga perioodi alguses. Seda tüüpi tehinguid ja sellist maksevoogu saab näha pensioniplaani saaja kontol. Koguväärtus on summa, milleni tulevikus makstavate maksete seeriad kasvavad, kui eeldada teatavat intressisummat, ja tulud suurenevad teatud aja jooksul järk-järgult. Tavalise annuiteedi tulevase väärtuse arvutamine on sellega identne, kuid ainus erinevus seisneb selles, et lisame lisa makseperioodi, mis tehakse alguses.
Annuiteedivormi kalkulaatori tulevikuväärtus
Võite kasutada järgmist annuiteedimäära kalkulaatorit
| Lk | |
| r | |
| n | |
| Annuiteedivormi tulevane väärtus | |
| Annuiteedivormi tulevane väärtus = | (1 + r) * P * (((1 + r) n - 1) / r) |
| = | (1 +0) * 0 * (((1 +0) 0 -1) / 0) = 0 |
Soovitatavad artiklid
See on olnud juhend annuiteedivormi tulevikuväärtuse leidmiseks. Siin arutatakse, kuidas koos praktiliste näidetega arvutada makstava annuiteedi tulevikuväärtust. Pakume ka allalaetava Exceli malliga annuiteedimäära kalkulaatorit Future Value. Lisateabe saamiseks võite vaadata ka järgmisi artikleid -
- Raha ajaväärtuse valemi juhend
- Nüüdisväärtuse teguri valemi näited
- Teabevahetuse valemi kalkulaator
- Tegevusvõimenduse kraadi valem