
Standardhälbe valemi näidis (sisukord)
- Valem
- Näited
Standardhälbe valem
Statistikas on standardhälve põhimõtteliselt mõõtühik, mille abil leitakse andmekogumi väärtused hajutatult andmekogumi keskväärtusest. See mõõdab selle andmepunkti kaugust ja keskmist. Mida kõrgem on standardhälve, seda suurem on dispersioon ja andmepunktid kipuvad keskmisest kaugel olema. Samamoodi tähendab madalam standardhälve, et andmepunktid on keskmisele lähemal. See on väga kasulik andmekogumite võrdlemisel, millel võib olla sama keskmine väärtus, kuid erinev vahemik.
Tavaliselt arvutage elanikkonna andmete standardhälve, kuid mõnikord on rahvastiku andmed nii suured, et selle jaoks pole standardhälvet võimalik leida. Sel juhul arvutatakse valimi standardhälve ja sellest saab populatsiooni standardhälbe representatiivne väärtus. Seega eeldame, et valim esindab üldkogumi õigesti ja keskendume selles artiklis valimi standardhälbele.
Oletame, et teil on andmekogu X koos andmepunktidega (X1, X2 …… ..Xn).
Elanikkonna standardhälbe valem on esitatud järgmiselt:
Population Standard Deviation = √ (Σ (X i – X m ) 2 / n )
Kui teile ei anta kogu populatsiooni ja teil on ainult valim (oletame, et X on populatsiooni valimi andmekogum), antakse valimi standardhälbe valem järgmiselt:
Sample Standard Deviation = √ (Σ (X i – X m ) 2 / (n – 1))
Kus:
- X i - andmekogumi i- ne väärtus
- X m - andmekogumi keskmine väärtus
- n - andmepunktide koguarv
Valem võib alguses tunduda segane, kuid selle kallal on tõesti vaja töötada. Järgmised sammud on näidise standardhälbe arvutamiseks järgmised:
- Leidke andmekogumis olevate punktide arv, st n
- Järgmine samm on proovi keskmise väärtuse leidmine. Põhimõtteliselt on see kõigi väärtuste keskmine.
- Pärast seda leidke iga andmepunkti jaoks erinevus keskmisest ja ruutke seejärel ruut.
- Summeerige kõik ülaltoodud etapis olevad väärtused ja jagage need n-1-ga.
- Viimane samm on ülaltoodud arvutatud ruutjuure mõõtmine.
Populatsiooni ja standardhälbe arvutamiseks on veel üks viis, kasutades populatsiooni standardhälbe jaoks funktsiooni STDEV.P () ja Exceli valimi standardhälbe funktsiooni STDEV.S ().
Standardhälbe valemi näidised (koos Exceli malliga)
Võtame näite, et paremini mõista proovi standardhälbe arvutamist.
Selle standardhälbe valemi Exceli malli saate alla laadida siit - standardhälbe valemi Exceli mallStandardhälbe valemi näidis - näide nr 1
Oletame, et meil on kaks näidisandmekogumit A ja B ning igaüks sisaldab 20 juhuslikku andmepunkti ja nende keskmine on sama. Arvutage andmekogumi A ja B proovi standardhälve.
Lahendus:
Keskmine arvutatakse järgmiselt:
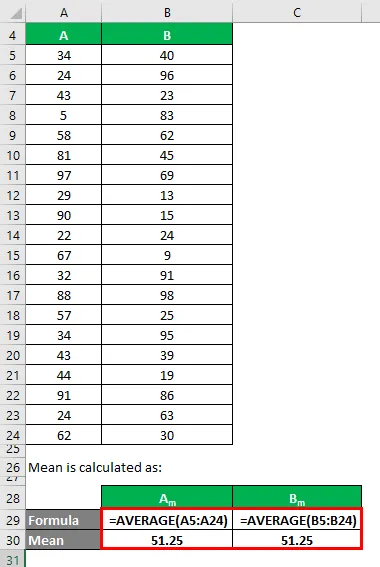
- Andmekogumi keskmine A = 51, 25
- Andmekogumi B keskmine = 51, 25
Nüüd peame arvutama erinevuse andmepunktide ja keskmise väärtuse vahel.
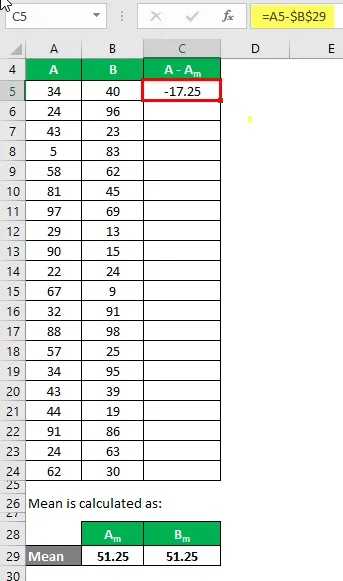
Samamoodi arvutage kõigi A-andmekogumite jaoks.
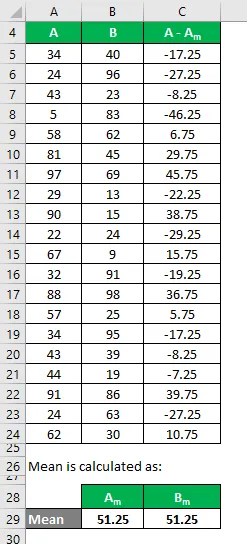
Samamoodi arvutage see ka andmekogumi B jaoks.
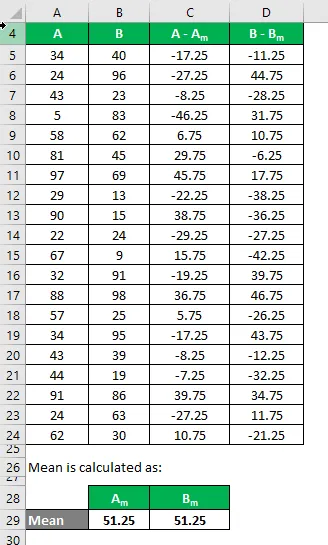
Arvutage erinevuse ruut nii andmekogumite A kui ka B jaoks.
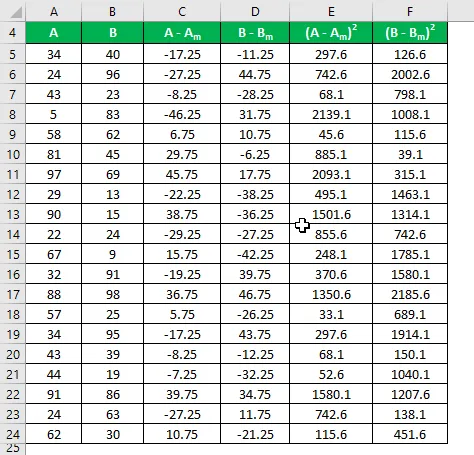
Proovi standardhälve arvutatakse järgmise valemi abil
Näite standardhälve = √ (Σ (X i - X m ) 2 / (n - 1))
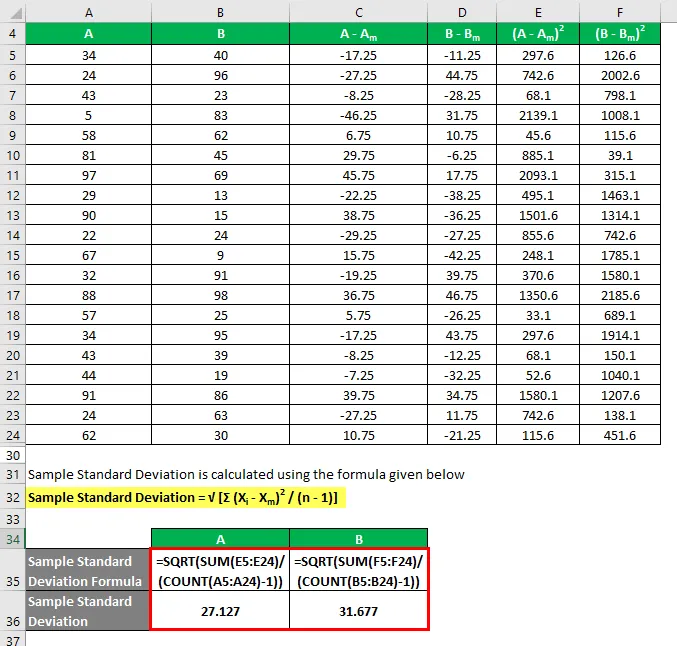
Nii et kui näete siin, ehkki mõlemal andmestikul on sama keskmine väärtus, on B-l standardhälve suurem kui A, mis tähendab, et B andmepunktid on hajutatud rohkem kui A.
Standardhälbe valemi näidis - näide nr 2
Ütleme, et olete väga riskikartlik investor ja soovite investeerida raha aktsiaturule. Kuna teie riskivalmidus on madal, soovite investeerida turvalistesse aktsiatesse, mille standardhälve on madalam. Teie finantsnõustaja on teile soovitanud 4 aktsiat, mille hulgast saate valida. Soovite nende 4 hulgast valida 2 varusid ja otsustate selle madalama standardhälbe alusel.
Teil on teavet nende viimase 15 aasta ajaloolise tulu kohta.
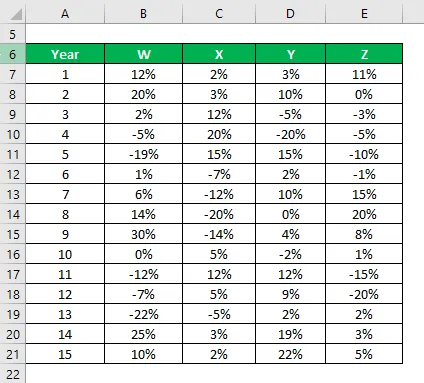
Lahendus:
Proovi standardhälve arvutatakse exceli valemi abil
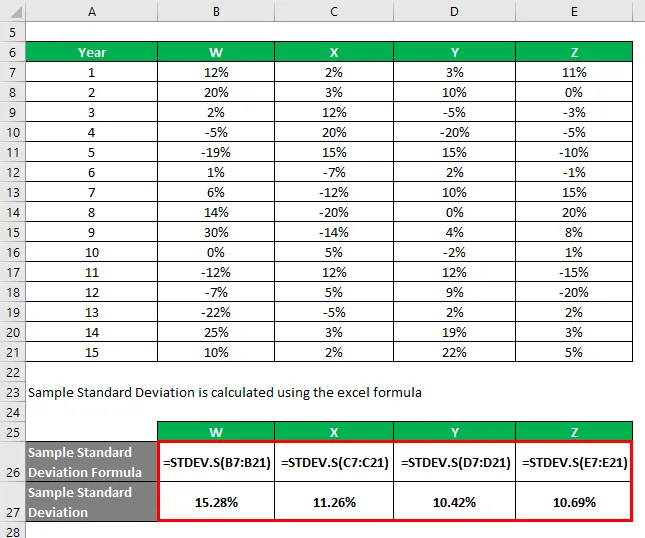
Teabe ja valimi standardhälbe põhjal valite investeerimiseks aktsiad Y ja Z, kuna neil on väikseim standardhälve.
Seletus
Arutame standardhälbe tähendust statistilisest seisukohast, kuid see mängib olulist rolli ka siis, kui räägime rahalisest aspektist. Rahanduses on see põhimõtteliselt investeeringuga kaasneva riski mõõt ja see, kui riskantne see investeering on. Investeerimisriski alusel saavad investorid seejärel arvutada minimaalse tulu, mida nad selle riski kompenseerimiseks vajavad. Nagu ülaltoodud näites, tähendab see, et kui Y ja Z on väiksema standardhälbega, tähendab see, et nende varude tootlus on vähem varieeruv, seega on nad vähem riskantsed. Ühest punktist standardhälbe tööriista kasutamisel peame meeles pidama, et äärmuslikud väärtused või kõrvalekalded mõjutavad seda väga. Need kõrvalekalded võivad standardhälbe väärtust väänata.
Standardhälbe valemi asjakohasus ja kasutamine
Standardhälve aitab investoritel ja analüütikutel leida investeeringu riski ja tulu suhe või Sharpe'i suhe. Põhimõtteliselt võib igaüks teenida riskivaba tootluse, investeerides riigikassasse ja riskivabadesse väärtpaberitesse. Kuid lisaks sellele on tulu ülemäärane tulu ja selle saavutamiseks peab Sharpe'i suhte mõõt olema riskitase:
Sharpe'i suhe = (investeeringutasuvus - riskivaba määr) / standardhälve
Sharpe'i suhte suurendamiseks on parem investeering.
Nagu me ütlesime, on standardhälve riski mõõt, kuid madalamat standardhälbe väärtust ei eelistata alati. Kui investoril on suurem riskivalmidus ja ta soovib investeerida agressiivsemalt, on ta nõus võtma rohkem riski ja eelistama suhteliselt suuremat standardhälvet kui riskikartlik investor. Nii et kõik sõltub sellest, millist riskitaset investor on nõus võtma.
Soovitatavad artiklid
See on olnud standardhälbe valemi näidis. Siin arutatakse, kuidas arvutada näidise standardhälvet koos praktiliste näidete ja allalaaditava excelimalliga. Lisateabe saamiseks võite vaadata ka järgmisi artikleid -
- Rahvastiku variatsioonvalemi näited
- Suhtelise standardhälbe kalkulaator
- Kuidas arvutada normaalset normaaljaotust?
- Binoomjaotuse arvutamine