Liitintressi näide - Praktilised näited valemiga

Sissejuhatus liitintressi näitesse

Liitintressidest on palju näiteid. Järgnev erinev liitintressi näide annab mõista tavalisemat tüüpi olukordades, kus liitintressi arvutatakse, ja kuidas seda sama arvutada. Kuna liitintressi saab arvutada mitmetes valdkondades ja olukordades, pole võimalik esitada kõiki näiteid. Allpool on toodud mõned liitintressi näited, kus on toodud erinevad olukorrad

Näited liitintressidest (Exceli malliga)

Võtame näite liitintressi arvutamise paremaks mõistmiseks.

Selle liitintressi näite Exceli malli saate alla laadida siit - liitintressi näidis Exceli mall. Allpool on toodud liitintressi näited.

Liitintressi näide -1

Harry soovib alustada säästu tema teenitud rahaga. Seejärel otsustab ta hoiustada esialgse summa 10 000 dollarit kõrge intressiga hoiukontole. Intressimäär on sel juhul 15% aastas, liites aastas. Praegu on Harry vanus 40 aastat ja ta kavatseb pensionile minna 60-aastaselt. See tähendab, et Harryl on 40-aastane ajahorisont, mille jooksul ta suudab huvi koguda. Arvutage välja rahasumma, mida Harry saab 60-aastaselt. Samuti koostage tabel, mis näitab aastaintressi ja konto väärtust.

Arvestades,

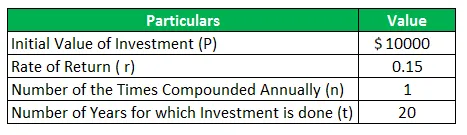
Lahendus:

Esitatud teavet kasutades arvutatakse liitintress ja 60-aastaselt saadav summa järgmiselt:

Investeeringu tulevase väärtuse arvutamine liitintressi valemi abil on järgmine:

A = P (1 + r / n) ^nt

A = 10 000 dollarit (1 + 0, 15 / 1) ^{1 * 20}
A = 10 000 dollarit (1 + 0, 15) ²⁰
A = 10 000 dollarit (1, 15) ²⁰
A = 10 000 dollarit * 16, 367
A = 163 665, 37 dollarit

Tabel aastaintressi ja konto väärtuse näitamiseks

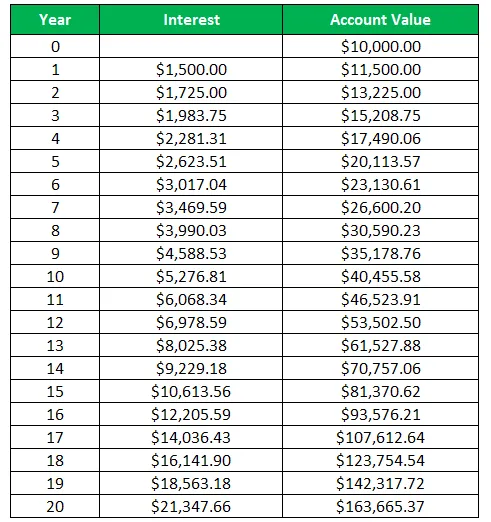
Siin arvutatakse intress järgmiselt:

Intress = Investeeringu algsumma * Intressimäär (r)
Intress = 10000 * 15%
Intress = 1500 dollarit

Samamoodi kõigi aastate jooksul.

ja konto väärtus arvutatakse järgmiselt:

Konto väärtus = investeeringu algsumma + intress
Konto väärtus = 10000 + 1500
Konto väärtus = 11500 dollarit

Samamoodi kõigi aastate jooksul.

Selles näites näeme, et algselt tehtud 10 000 dollari suuruse investeeringu kontoväärtuseks saab 20-aastase perioodi lõpus 163 665, 37 dollarit. See tõstab esile liitmise võimet, kuna liitintressi abil korrutas Harry oma raha mitmekordselt, ilma et peaks investeeringut aktiivselt juhtima. Siin suutis Harry teenida intressi ka varem teenitud intresside pealt.

Ühendi intressinäide -2

Sam teeb esialgse investeeringu 10 000 dollarit 5 aastaks. Ta soovib teada, kui palju investeeringuid ta viie aasta pärast teenib, kui investeering teenib 6% aastas tootlust nädalas.

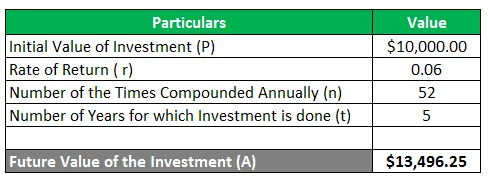
Arvestades,

Esitatud teavet kasutades arvutatakse liitintress ja pärast 5-aastast perioodi saadav summa järgmiselt:

Lahendus:

Investeeringu tulevase väärtuse arvutamine liitintressi valemi abil on järgmine:

A = P (1 + r / n) ^nt

A = 10 000 dollarit (1 + 0, 6 / 52) ^{52 * 5}

A = 10 000 dollarit (1 + 0, 00115) ²⁶⁰

A = 10 000 dollarit (1, 00115) ²⁶⁰

A = 10 000 dollarit * 1, 3496

A = 13 496, 25 dollarit

Käesolevas näites näeme, et algselt tehtud 10 000 dollari suuruse investeeringu kontoväärtus muutub 13 496, 25 dollariks 5-aastase perioodi lõpus, kui segu koostatakse igal nädalal. Liitmine suurendab investeeringu väärtust perioodi lõpus, kuna intressi teenitakse ka varem teenitud intressilt. Siin toimub liitmine 52 korda, kuna aastas on 52 nädalat.

Järeldus - liitintressi näide

Liitintress pakub rohkem intressi kui lihtsad intressid, kuna selle saamiseks arvestatakse tasumata intressilt intressi, sealhulgas intressi, erinevalt lihtintressist, kus intressi võetakse algselt põhisummalt ja intressi pealt intressi ei nõuta. Liitmise võimsus aitab investeeringut kasvatada suurema kiirusega, millel on eksponentsiaalse funktsiooni omadused. See on tingitud asjaolust, et vaatamata investeeringu tasumisele investeeritakse nad uuesti, et kiiremini kasvada. Seda kasutatakse väga sageli tavapärastes äritavades, olgu see siis laenu või hoiuse puhul. Pealegi on kasvu määravaks teguriks ka see, kui sageli segatakse. Oletame, et kui mingil kindlal kiirusel on liitmise sagedus kuus, siis on selle aastapõhine määr suurem kui liitumissageduse määramine poolaastas või igal aastal.

Soovitatavad artiklid

See on olnud liitintressi näite juhend. Siin arutatakse, kuidas arvutada liitintresse valemi abil koos praktiliste näidetega. Võite lisateabe saamiseks vaadata ka järgmisi artikleid -