
Poissoni jaotuse valem (sisukord)
- Valem
- Näited
- Kalkulaator
Mis on Poissoni jaotuse valem?
Tõenäosuses ja statistikas on kolme tüüpi jaotusi, mis põhinevad pidevatel ja diskreetsetel andmetel - normaal-, binomiaal- ja Poissoni jaotused. Tavaline jaotus on sageli nagu kõver. Poissoni jaotust nimetatakse sageli haruldaste sündmuste jaotuseks. Seda kasutatakse peamiselt toimuvate sündmuste tõenäosuse prognoosimiseks vastavalt sellele, kui sageli on sündmus minevikus juhtunud. See annab võimaluse teatud arvu sündmuste toimumiseks teatud perioodil. Seda kasutatakse paljudes reaalsetes olukordades.
Allpool on toodud Poissoni jaotuse leidmise valem:
P(x) = (e -λ * λ x) / x!
X = 0, 1, 2, 3…
See katse arvestab üldiselt piirkonnas toimunud vahemaa, vahemaa või ruumala jooksul juhtunud sündmuste arvu. Koos sellega võib leida sündmuste ahela, mis pole midagi muud kui sama sündmuse sündmuste ahel konkreetsel ajavahemikul. Poissoni jaotusel on järgmised ühised omadused.
- Sündmus võib toimuda suvalisel arvul kellaaegadel igal ajal.
- Üritusel võib arvestada mis tahes mõõtmeid, nagu maht, pindala, vahemaa ja aeg.
- Kõigi ülalnimetatud meetmete korral on sündmuse toimumise tõenäosus sama.
- Iga sündmus ei sõltu kõigist teistest sündmustest, mis tähendab, et sündmuse toimumise tõenäosus ei mõjuta teisi samal ajal toimuvaid sündmusi.
Poissoni jaotusvalemi näited
Võtame näite, et mõista paremini Poissoni jaotuse arvutamist.
Selle Poissoni jaotuse valemi Exceli malli saate alla laadida siit - Poissoni jaotuse valemi Exceli mallPoissoni jaotuse valem - näide # 1
Rongiliikluse ajal juhtub raudteejaama platvormil keskmiselt 7 õnnetust aastas. Selleks, et tuvastada tõenäosus, et samal platvormil toimub sel aastal täpselt 4 vahejuhtumit, võib kasutada Poissoni jaotuse valemit.
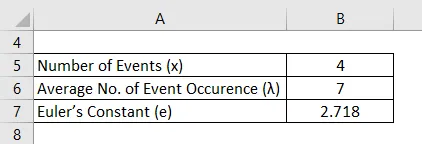
Lahendus:
Poissoni jaotus arvutatakse järgmise valemi abil
P (x) = (e-X * λ x) / x!
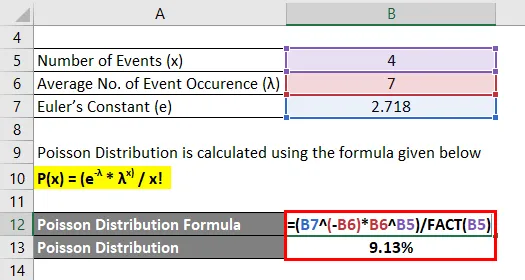
- P (4) = (2, 718 -7 * 7 4) / 4!
- P (4) = 9, 13%
Antud näite puhul on tõenäosus, et juhtub täpselt sama palju õnnetusi, kui sel aastal võib juhtuda 9, 13% .
Poissoni jaotuse valem - näide # 2
Masinakirjutaja tehtud trükivigade arvul on Poissoni jaotus. Vigu tehakse iseseisvalt, keskmiselt 2 lehekülje kohta. Leidke tõenäosus, et kolmeleheküljeline kiri ei sisalda vigu.
Siin on keskmine määr lehel = 2 ja keskmine määr 3 lehel (λ) = 6
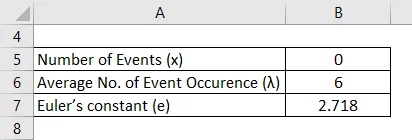
Lahendus:
Poissoni jaotus arvutatakse järgmise valemi abil
P (x) = (e-X * λ x) / x!
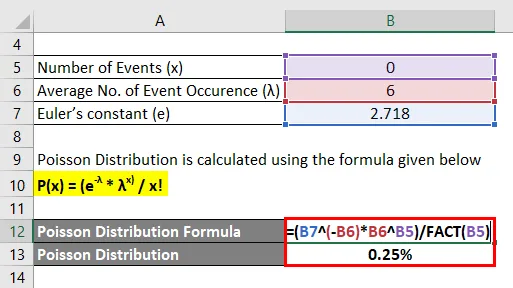
- P (0) = (2, 718 -6 * 6 0 ) / 0!
- P (0) = 0, 25%
Seega on 0, 25% tõenäosus, et 3 lehekülje korral vigu ei tehta.
Märkus : x 0 = 1 (väärtus 0 on alati 1) ; 0! = 1 (nullfaktoriaal on alati 1)Seletus
Allpool on toodud samm-sammuline lähenemisviis Poissoni jaotusvalemi arvutamiseks.
1. samm: e on Euleri konstant, mis on matemaatiline konstant. Üldiselt on e väärtus 2, 718 .
2. samm: X on tegelikult aset leidnud sündmuste arv. Sellel võivad olla järgmised väärtused. x = 0, 1, 2, 3…
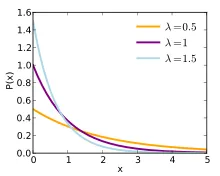
3. samm: λ on sündmuste keskmine (keskmine) arv (tuntud ka kui “Poissoni jaotuse parameeter”). Kui võtta λ => 1, 2, 3, 4, 5 arvutamiseks lihtne näide. Kui kasutate sama andmekomplekti ülaltoodud valemis, on n = 5, seega = = (1 + 2 + 3 + 4 + 5) / 5 = 3. Suure hulga andmete korral pole mediaani käsitsi otsimine võimalik. Seega on väga oluline kasutada valemit suure hulga andmekogumite jaoks. Poissoni jaotuse arvutamisel saame tavaliselt keskmise arvu otse. Põhinedes λ väärtusel, võib Poissoni graafik olla kas ühemoodiline või bimodaalne nagu allpool.
4. samm: x! on toimunud sündmuste faktoorium x. Allpool on toodud näide, kuidas arvutada antud numbri jaoks faktoriaal.
Kui võtta tegeliku andmekogumi Faktoriaalse arvutamiseks lihtne näide => 1, 2, 3, 4, 5.
- x! = x * (x-1) * (x-2) * (x-3) * …… 3 * 2 * 1
- 5! = 5 * (5-1) * (5-2) * (5-3) * (5-4)
- 5! = 5 * 4 * 3 * 2 * 1
- 5! = 120
Poissoni turustusvalemi asjakohasus ja kasutamine
Poissoni jaotus võib toimida juhul, kui andmekogum on diskreetne jaotus, iga juhtum on muudest juhtumistest sõltumatu, kirjeldab diskreetseid sündmusi intervalli jooksul, iga intervalli sündmused võivad ulatuda nullist lõpmatuseni ja tähendada, et esinemiste arv peab olema konstantse kogu protsessi vältel. Sõltuvalt parameetri (λ) väärtusest võib jaotus olla ühe- või kaheliigiline. Poissoni jaotus on diskreetne jaotus, mis tähendab, et sündmuse saab kuulutada toimunuks või mitte kui toimuvaks, see tähendab, et arvu saab öelda ainult täisarvudes. Selle mudeli hulka ei kuulu sündmuse murrangulised juhtumid. Tulemusi võib liigitada õnnestumisteks või ebaõnnestumisteks. Seda kasutatakse laialdaselt järgmiste riikide maailmas:
- Data Analytics andmete ennustavaks analüüsiks
- Aktsiaturu ennustused
- Müügituru ennustused
- Tarne- ja nõudluse ahela prognoosid
- Kergesti saadaval Amazon Web Services (AWS) platvormidel
- Ärikindlustuse ülevaatamine ja hindamine
Muud Poissoni jaotuse rakendused pärinevad avatumatest probleemidest. Näiteks võib seda kasutada kõnekeskuses vajalike ressursside minimaalse hulga kindlaksmääramisel, lähtudes keskmistest vastuvõetud ja ootel kõnedest. Lühidalt, rakenduste loendit saab üha enam lisada, kuna seda kasutatakse kogu maailmas praktilisel statistilisel eesmärgil.
Poissoni jaotuse valemi kalkulaator
Võite kasutada järgmist Poissoni jaotuskalkulaatorit
| λ | |
| x | |
| P (x) | |
| P (x) = | (e- λ * λ x ) / x! | |
| (0 -0 * 0 0 ) / 0! = | 0 |
Poissoni jaotusvalem Excelis (koos Exceli malliga)
Siinkohal teeme veel ühe näite Poissoni jaotusest Excelis. See on väga lihtne ja lihtne.
Arvutage Poissoni jaotus Excelis funktsiooni POISSON.DIST abil.
Allpool on toodud Excelis Poissoni jaotuse valemi süntaks.

Poissoni jaotusel on järgmine argument:
Kus,
- x = nende juhtumite arv, mille tõenäosust on vaja teada.
- Keskmine = keskmine juhtumite arv ajavahemikul.
- Kumulatiivne = Selle väärtus on vale, kui vajame sündmuse täpset esinemist, ja tõene, kui juhuslike sündmuste arv jääb vahemikku 0 kuni see sündmus.

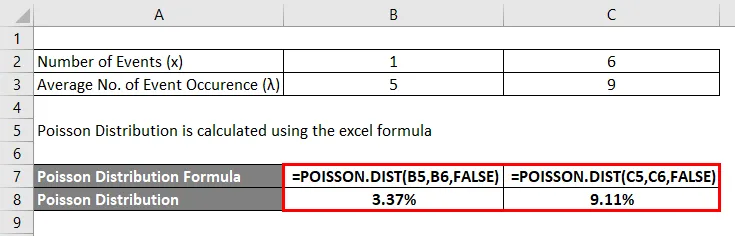
Poissoni jaotust arvutatakse exceli valemi abil
Soovitatavad artiklid
See on olnud Poisson Distribution Formula juhend. Siin käsitleme kuidas arvutada Poissoni jaotust koos praktiliste näidetega. Pakume ka allalaaditava Exceli malliga Poissoni jaotuse kalkulaatorit. Lisateabe saamiseks võite vaadata ka järgmisi artikleid -
- Tavalise normaaljaotuse valemi kalkulaator
- T-jaotuse valemi arvutamine Exceli malliga
- Valem variatsioonianalüüsi arvutamiseks
- Mis on vara puhasväärtuse valem?