Lineaarse regressiooni ja logistilise regressiooni erinevus
Järgmine artikkel Lineaarne regressioon vs logistiline regressioon pakub kõige olulisemaid erinevusi mõlema vahel, kuid enne vaatame, mida regressioon tähendab?
Regressioon
Regressioon on põhimõtteliselt statistiline meede, et määrata kindlaks sõltuvuse muutuja, st väljundi Y ja muude sõltumatute muutujate, st X 1, X 2 jne seose tugevus. Regressioonianalüüsi kasutatakse põhimõtteliselt ennustamiseks ja prognoosimiseks.
Mis on lineaarne regressioon?
Lineaarne regressioon on algoritm, mis põhineb masinõppe juhendatud õppevaldkonnal. See pärib lineaarse seose oma sisendmuutujate ja ühe väljundmuutuja vahel, kui väljundmuutuja on olemuselt pidev. Seda kasutatakse väljundi väärtuse ennustamiseks, ütleme Y sisenditest, ütleme X. Kui arvestada ainult üksikut sisendit, nimetatakse seda lihtsaks lineaarseks regressiooniks.
Selle võib jagada kahte peamisse kategooriasse:
1. Lihtne regressioon
Toimimispõhimõte: peamine eesmärk on välja selgitada valimi andmetele kõige paremini vastava sirge võrrand. See võrrand kirjeldab algebraliselt kahe muutuja vahelist suhet. Kõige paremini sobivat sirget nimetatakse regressioonijooneks.
Y = β 0 + β 1 X
Kus,
β tähistab tunnuseid
P 0 tähistab pealtkuulamist
β1 tähistab tunnuse X koefitsienti
2. Mitme muutuja regressioon
Seda kasutatakse korrelatsiooni ennustamiseks enam kui ühe sõltumatu muutuja ja ühe sõltuva muutuja vahel. Enam kui kahe sõltumatu muutujaga regressioon põhineb kuju sobitamisel mitmemõõtmelise graafiku andmete konstellatsioonile. Regressiooni kuju peaks olema selline, et see vähendaks kuju kaugust igast andmepunktist.
Lineaarse suhte mudelit saab matemaatiliselt esitada järgmiselt:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Kus,
β tähistab tunnuseid
P 0 tähistab pealtkuulamist
β1 tähistab tunnuse X1 koefitsienti
β n tähistab tunnuse Xn koefitsienti
Lineaarse regressiooni eelised ja puudused
Allpool on toodud eelised ja puudused:
Eelised
- Oma lihtsuse tõttu kasutatakse seda laialdaselt ennustuste ja järelduste modelleerimiseks.
- See keskendub andmete analüüsile ja andmete eeltöötlusele. Niisiis, see tegeleb erinevate andmetega, ilma et peaksite mudeli üksikasjade pärast vaeva nägema.
Puudused
- See töötab tõhusalt, kui andmeid tavaliselt levitatakse. Seega tuleb efektiivse modelleerimise puhul vältida kollineaarsust.
Mis on logistiline regressioon?
See on regressiooni vorm, mis võimaldab diskreetseid muutujaid ennustada pidevate ja diskreetsete ennustajate segu abil. Selle tulemuseks on sõltuvate muutujate ainulaadne teisendus, mis mõjutab mitte ainult hindamisprotsessi, vaid ka sõltumatute muutujate koefitsiente. Selles käsitletakse sama küsimust, mida mitme regressiooniga tehakse, kuid ilma ennustajate jaotuseelduseta. Logistilises regressioonis on tulemusmuutuja binaarne. Analüüsi eesmärk on hinnata mitme selgitava muutuja mõju, mis võivad olla numbrilised või kategoorilised või mõlemad.
Logistilise regressiooni tüübid
Allpool on toodud kaks logistilise regressiooni tüüpi:
1. Binaarne logistiline regressioon
Seda kasutatakse siis, kui sõltuv muutuja on kaheharuline, st nagu kahe haruga puu. Seda kasutatakse juhul, kui sõltuv muutuja ei ole parameetriline.
Kasutatakse siis
- Kui puudub lineaarsus
- Sõltuval muutujal on ainult kaks taset.
- Kui mitme muutujaga normaalsus on kaheldav.
2. Multinomaalne logistiline regressioon
Multinomaalne logistiline regressioonanalüüs eeldab, et sõltumatud muutujad peaksid olema metrilised või dihhotoomsed. See ei tee mingeid eeldusi sõltumatute muutujate lineaarsuse, normaalsuse ja dispersiooni homogeensuse kohta.
Seda kasutatakse juhul, kui sõltuval muutujal on rohkem kui kaks kategooriat. Seda kasutatakse mittemeetrilisest sõltuva muutuja ja meetriliste või dihhotoomsete sõltumatute muutujate vaheliste seoste analüüsimiseks, seejärel võrreldakse mitu rühma binaarsete logistiliste regressioonide kombinatsiooni abil. Lõpuks pakub see mõlema võrdluse jaoks koefitsientide komplekti. Võrdlusrühma koefitsientideks loetakse kõik nullid. Lõpuks ennustatakse suurima võimaliku tõenäosuse põhjal.
Logistilise regressiooni eelis: see on väga tõhus ja laialdaselt kasutatav tehnika, kuna see ei vaja palju arvutusressursse ega vaja häälestamist.
Logistilise regressiooni puudus: seda ei saa kasutada mittelineaarsete probleemide lahendamiseks.
Lineaarse regressiooni ja logistilise regressiooni võrdlus (infograafika)
Allpool on toodud 6 peamist erinevust lineaarse regressiooni ja logistilise regressiooni vahel 
Peamine erinevus lineaarse regressiooni ja logistilise regressiooni vahel
Arutleme mõne peamise põhierinevuse vahel lineaarse regressiooni ja logistilise regressiooni vahel
Lineaarne regressioon
- See on lineaarne lähenemine
- See kasutab sirgjoont
- See ei saa võtta kategoorilisi muutujaid
- See eirab tähelepanekuid, kus puuduvad arvulise sõltumatu muutuja väärtused
- Väljund Y antakse kui
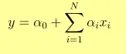
- X ühiku suurenemine suurendab Y α võrra
Rakendused
- Toote hinna ennustamine
- Skoori ennustamine matšis
Logistiline regressioon
- See on statistiline lähenemisviis
- See kasutab sigmoidset funktsiooni
- See võib võtta kategoorilisi muutujaid
- Ta võib otsuseid vastu võtta ka siis, kui puuduvad puuduvate väärtustega vaatlused
- Väljund Y antakse kui, kus z antakse kui
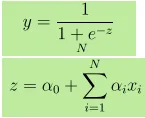
- X ühiku suurenemine 1 võrra suurendab Y α log koefitsientide võrra
- Kui P on sündmuse tõenäosus, siis (1-P) on tõenäosus, et see ei toimu. Edu koefitsiendid = P / 1-P
Rakendused
- Ennustatakse, kas täna sajab vihma või mitte.
- Selle ennustamine, kas e-kiri on rämpspost või mitte.
Lineaarse regressiooni vs logistilise regressiooni võrdlustabel
Arutleme lineaarse regressiooni ja logistilise regressiooni ülemist võrdlust
|
Lineaarne regressioon |
Logistiline regressioon |
| Seda kasutatakse regressiooniprobleemide lahendamiseks | Seda kasutatakse klassifitseerimisprobleemide lahendamiseks |
| See modelleerib sõltuva muutuja ja ühe või mitme sõltumatu muutuja vahelist suhet | See ennustab sellise tulemuse tõenäosust, millel võib väljundis olla ainult kaks väärtust: 0 või 1 |
| Prognoositav väljund on pidev muutuja | Prognoositav väljund on diskreetne muutuja |
| Prognoositav väljund Y võib ületada vahemikku 0 ja 1 | Prognoositav väljund Y jääb vahemikku 0 ja 1 |
 | 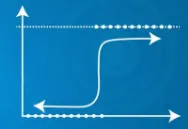 |
| Prognoositav väljund Y võib ületada vahemikku 0 ja 1 | Prognoositav väljund |
Järeldus
Kui funktsioonid ei aita ennustada või kui need on üksteisega väga korrelatsioonis, lisab see mudelile müra. Seega tuleb eemaldada funktsioonid, mis mudelile piisavalt kaasa ei aita. Kui sõltumatud muutujad on tugevas korrelatsioonis, võib see põhjustada mitme kollineaarsuse probleemi, mille saab lahendada, käivitades eraldi mudelid iga sõltumatu muutujaga.
Soovitatavad artiklid
See on olnud teemaks Lineaarne regressioon vs Logistiline regressioon. Siin käsitleme lineaarse regressiooni vs logistilise regressiooni peamisi erinevusi infograafikaga ja võrdlustabelit. Võite lisateabe saamiseks vaadata ka järgmisi artikleid -
- Andmeteadus vs andmete visualiseerimine
- Masinõpe vs närvivõrk
- Juhendatud õpe vs sügav õpe
- Logistiline regressioon R-s