
Sissejuhatus DFS-i algoritmi
DFS on tuntud kui esimese sügavuse otsingu algoritm, mis pakub samme graafiku iga sõlme läbimiseks ilma ühtegi sõlme kordamata. See algoritm on sama, mis puu sügavuse esimene läbimine, kuid erineb selle poolest, et säilitada tõeväärtust, et kontrollida, kas sõlme on juba külastatud või mitte. See on oluline graafiku läbimisel, kuna graafikus on ka tsüklid. Selles algoritmis hoitakse virna riputatud sõlmede hoidmiseks läbimise ajal. Seda nimetatakse sellepärast, et sõidame kõigepealt iga külgneva sõlme sügavusele ja jätkame seejärel teise külgneva sõlme läbimist.
Selgitage DFS-i algoritmi
See algoritm on vastuolus BFS-i algoritmiga, kus külastatakse kõiki külgnevaid sõlme ja naabrite külgnevaid sõlme. Ta alustab graafiku uurimist ühest sõlmest ja uurib selle sügavust enne tagasiulatuvust. Selles algoritmis võetakse arvesse kahte asja:
- Vertexi külastamine: graafiku tipu või sõlme valimine, mida mööda liikuda.
- Vertexi uurimine: läbib kõik selle tipuga külgnevad sõlmed.
Pseudo-kood esimese sügavuse otsingu jaoks :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
Lineaarne läbipääs on olemas ka DFS-i jaoks, mida saab rakendada kolmel viisil:
- Eeltellimus
- Korras
- PostOrder
Tagurpidi postitamine on väga kasulik viis liikumiseks ja seda kasutatakse nii topoloogilises sortimises kui ka erinevates analüüsides. Samuti hoitakse virna nende sõlmede hoidmiseks, mille uurimine on veel pooleli.
Graafiku liikumine DFS-is
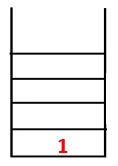
DFS-is järgitakse graafiku läbimiseks järgmisi samme. Näiteks antud graafiku korral alustame liikumist 1-st:
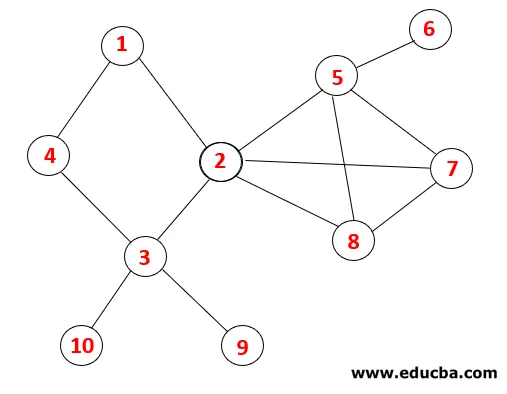
| Korstnat | Läbikäikude järjestus | Katkev puu |
| 1 |  |
|
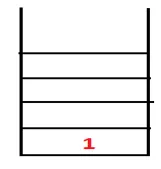 | 1, 4 |  |
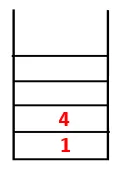 | 1, 4, 3 |  |
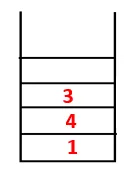 | 1, 4, 3, 10 | 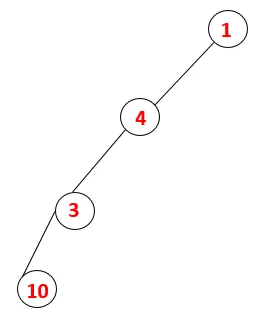 |
 | 1, 4, 3, 10, 9 | 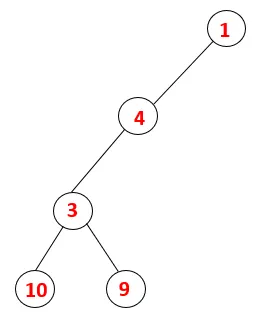 |
 | 1, 4, 3, 10, 9, 2 | 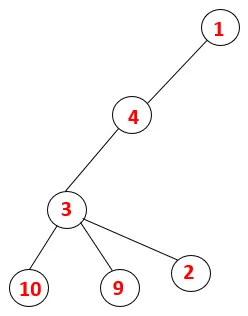 |
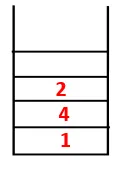 | 1, 4, 3, 10, 9, 2, 8 |  |
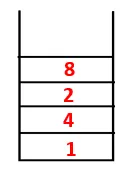 | 1, 4, 3, 10, 9, 2, 8, 7 | 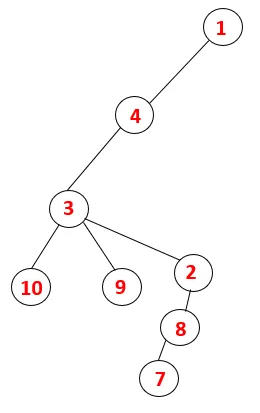 |
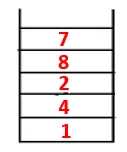 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
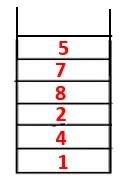 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 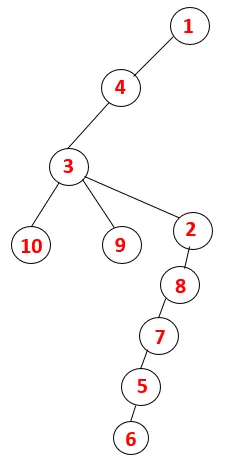 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 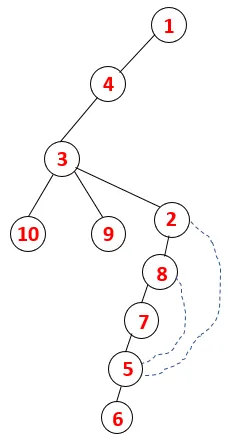 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
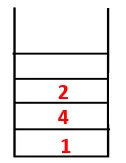 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 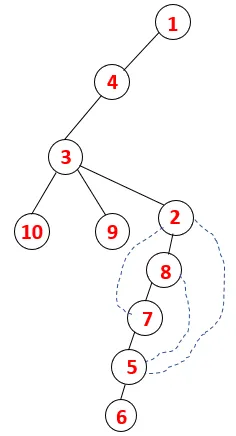 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 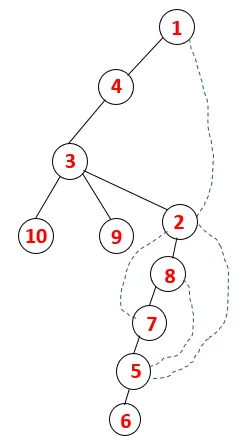 |
DFS-i algoritmi selgitus
Allpool on toodud sammud DFS-i algoritmi eeliste ja puudustega:
1. samm: 1. sõlme külastatakse ja see lisatakse jadasse, samuti kattepuu.
2. samm: uuritakse 1 külgnevaid sõlme, mis on 4, seega surutakse 1 virna ja 4 lükatakse järjestusesse, samuti kattepuusse.
3. samm: uuritakse ühte 4 külgnevatest sõlmedest ja seega lükatakse 4 virna ja 3 siseneb jada ja ulatuslikku puusse.
4. samm: uuritakse 3 külgnevaid sõlme, surudes selle virnale ja 10 siseneb jada. Kuna 10-le pole külgnevat sõlme, hüppatakse virnast välja 3.
5. samm: uuritakse veel ühte külgnevat 3 sõlme ja 3 lükatakse virnale ja külastatakse 9. Ühtegi kõrvalasuvat sõlme 9 seega 3 ei hüppata välja ja külastatakse viimast külgnevat sõlme 3 st 2.
Sarnast protsessi järgitakse kõigi sõlmede korral, kuni virn tühjeneb, mis näitab läbimisalgoritmi peatumistingimust. - -> Katkendliku puu punktiirjooned tähistavad graafikul olevaid tagumisi servi.
Sel moel läbivad kõik graafi sõlmed ühegi sõlme kordamiseta.
Eelised ja puudused
- Eelised: Selle algoritmi jaoks on vaja vähem mälu. Vähem keerukas ruum ja aeg kui BFS-il.
- Puudused: lahendus pole garanteeritud Rakendused. Topoloogiline sorteerimine. Graafiku sildade leidmine.
Näide DFS-i algoritmi rakendamiseks
Allpool on näide DFS-i algoritmi rakendamiseks:
Kood:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
Väljund:
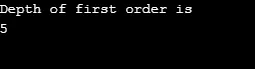
Ülaltoodud programmi seletus: Tegime 5 tipuga (0, 1, 2, 3, 4) graafiku ja kasutasime kõigi külastatud tippude jälgimiseks külastatud massiivi. Seejärel kordub iga sõlme puhul, mille külgnevad sõlmed on olemas, sama algoritm, kuni kõiki sõlme külastatakse. Seejärel naaseb algoritm tippu kutsumise juurde ja hüppab selle virnast välja.
Järeldus
Selle graafiku mäluvajadus on BFS-iga võrreldes väiksem, kuna säilitada on vaja ainult ühte virna. Selle tulemusel genereeritakse DFS-i hõlmav puu ja läbitav jada, kuid see pole konstantne. Sõltuvalt valitud lähtepunktist ja uurimist tipust on võimalik mitu transversaalset jada.
Soovitatavad artiklid
See on DFS-i algoritmi juhend. Siin käsitleme samm-sammult selgitamist, sirvime graafikut plussi ja miinustega tabelina. Lisateavet leiate ka meie muudest seotud artiklitest -
- Mis on HDFS?
- Süvaõppe algoritmid
- HDFS-i käsud
- SHA algoritm