
Z Testimisstatistika valem (sisukord)
- Valem
- Näited
- Kalkulaator
Mis on Z-testi statistika valem?
Z Testimisstatistika on statistiline protseduur, mida kasutatakse alternatiivse hüpoteesi testimiseks nullhüpoteesi alusel. See on mis tahes statistiline hüpotees, mida kasutatakse, et teha kindlaks, kas kahe valimi keskmine on erinev, kui dispersioonid on teada ja valim on suur. Z Test teeb kindlaks, kas valimi ja populatsiooni keskmiste vahel on oluline erinevus. Z Test, mida tavaliselt kasutatakse suurte proovidega seotud probleemide lahendamiseks. Nimetatud häirest tulenev nimetus "z test" on tehtud tavalisest normaaljaotusest ja "Z" on traditsiooniline sümbol, mida kasutatakse tavalise normaalse juhusliku muutuja tähistamiseks. Proovi järgi arvutatud Z-testi valem tähendab miinus populatsiooni keskmist, jagatud populatsiooni standardhälbe ja valimi suurusega. Kui valimi suurus on üle 30 ühiku, tuleb sel juhul teha z-test. Matemaatiliselt z testi valem on esitatud järgmiselt:
Z Test = (x̄ – μ) / ( σ / √n)
Siin
- x̄ = proovi keskmine
- μ = populatsiooni keskmine
- σ = rahvastiku standardhälve
- n = vaatluste arv
Z-testi statistika valemi näited (Exceli malliga)
Võtame näite Z testi statistika valemi arvutamise paremaks mõistmiseks.
Selle Z-testi statistika valemi Exceli malli saate alla laadida siit - Z-statistika statistika valemi Exceli mallZ Testi statistika valem - näide # 1
Oletame, et inimene soovib kontrollida või testida, kas tee ja kohv on mõlemad linnas võrdselt populaarsed. Sel juhul saab ta tulemuste saamiseks kasutada testtesti meetodit, võttes linnast umbes 500 valimi, millest arvatakse, et 280 on teejoojad. Selle hüpoteesi kontrollimiseks saab ta kasutada z-testi meetodit.
Kooli direktor väidab, et tema kooli õpilased on intelligentsemad kui keskmiselt ja juhusliku valimi 30 õpilase IQ-skooride keskmine skoor on 112, 5 ja keskmine populatsiooni IQ on 100, standardhälbega 15. Kas põhinõude toetuseks on piisavalt tõendeid? ?
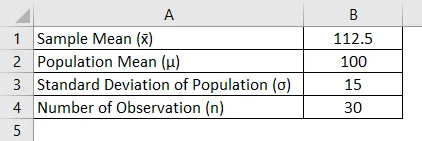
Lahendus:
Z Testimisstatistika arvutatakse järgmise valemi abil
Z test = (x̄ - μ) / ( σ / √n)
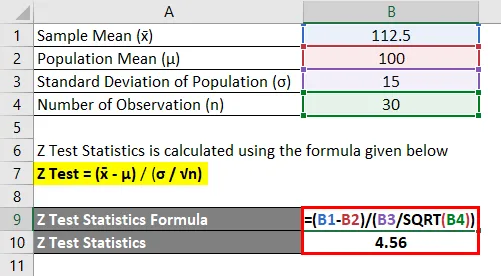
- Z test = (112, 5–100) / (15 / √30)
- Z test = 4, 56
Võrrelge z-testi tulemusi z-testi standardtabeliga ja selles näites võite järeldada, et nullhüpotees lükatakse tagasi ja peamine väide on õige.
Z Testi statistika valem - näide nr 2
Oletame, et investor, kes soovib analüüsida ettevõtte aktsiate keskmist päevane tootlus on suurem kui 1% või mitte? Nii et investorid valisid juhusliku valimi 50 ja tulu arvutatakse ning selle keskmine on 0, 02 ja investorite keskmine standardhälve on 0, 025.
Niisiis on sel juhul nullhüpotees, kui keskmine on 3% ja alternatiivne hüpotees on, et keskmine tootlus on suurem kui 3%. Investorid eeldavad, et kahepoolse testina valitakse alfa väärtus 0, 05% ja kummaski sabas on 0, 025% valimist ning alfa kriitiline väärtus on kas 1, 96 või -1, 96. Seega, kui Z-testi tulemus on väiksem või suurem kui 1, 96, lükatakse nullhüpotees tagasi.
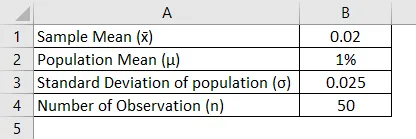
Lahendus:
Z Testimisstatistika arvutatakse järgmise valemi abil
Z test = (x̄ - μ) / ( σ / √n)
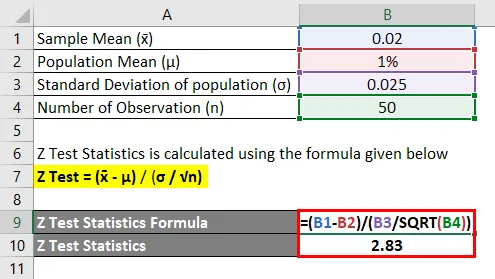
- Z test = (0, 02 - 1%) / (0, 025 / √50)
- Z test = 2, 83
Ülaltoodud arvutuse põhjal jõuavad investorid järeldusele ja ta lükkab nullhüpoteesi tagasi, kuna z tulemus on suurem kui 1, 96 ja tuleb analüüsi, et aktsia keskmine päevane tootlus on suurem kui 1%.
Z Testi statistika valem - näide # 3
Kindlustusselts vaatab praegu läbi oma praegused poliisi määrad, kui nad algselt määravad intressimäära, millesse nad usuvad, et keskmine kahjusumma on maksimaalselt 180000 Rs. Ettevõtte jaoks on muret tõeline keskmine, mis on sellest tegelikult kõrgem. Ettevõte valib juhuslikult 40 proovi nõuet ja arvutab valimi keskmise väärtuse Rs 195000, eeldades, et nõude standardhälve on Rs 50000 ja seada alfa väärtuseks 0, 05. Nii et z-test, mis tuleb kindlustusseltsi nägemiseks teha, peaks olema mures või mitte.
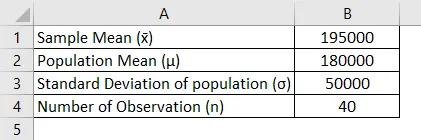
Lahendus:
Z Testimisstatistika arvutatakse järgmise valemi abil
Z test = (x̄ - μ) / ( σ / √n)
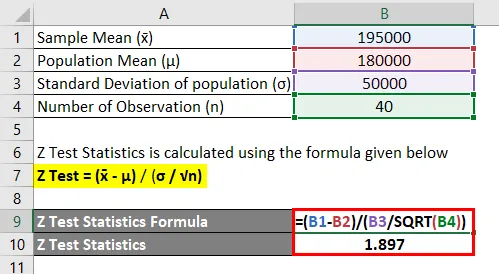
- Z test = (195000–180000) / (50000 / √40)
- Z test = 1, 897
1. samm Määrake hüpotees Null
2. etapp arvutage testi statistika
Nii et kui paned kõik saadaolevad arvud z-testi valemisse, annab see z-testi tulemuseks 1, 897
3. samm Määrake tagasilükkamise piirkond
Kui arvestada alfa väärtusega 0, 05, ütleme, et hülgamispiirkond on 1, 65
4. samm - tehke järeldus
Z-testi tulemuste põhjal näeme, et 1, 897 on suurem kui tagasilükkamispiirkond 1, 65, seega ei aktsepteeri ettevõte nullhüpoteesi ja kindlustusselts peaks oma praeguse poliitika pärast muretsema.
Seletus
- Esiteks määrake valimi keskmine (See on kõigi juhuslike valimite kaalutud keskmine).
- Määrake populatsiooni keskmine väärtus ja lahutage sellest valimi keskmine väärtus.
- Seejärel jagage saadud väärtus standardhälbega, jagatud arvu vaatluste ruutjuurega.
- Kui ülaltoodud toimingud on tehtud, arvutatakse z testi statistika tulemused.
Z-testi statistika valemi asjakohasus ja kasutamine
Z-testi kasutatakse tavalise juhusliku muutuja keskväärtuse võrdlemiseks kindlaksmääratud väärtusega. Z-test on kasulik või kasutatav juhul, kui proov on suurem kui 30 ja populatsiooni erinevus on teada. Z-test on parim eeldusel, et proovi keskmise jaotus on normaalne. Z-testi rakendatakse juhul, kui on seatud teatud tingimused, vastasel juhul peame kasutama teisi teste ja kõikumisi z-testis ei eksisteeri. Populatsiooni keskmise eriväärtuse hüpoteesi kontrollimiseks kasutatakse ühe testi Z testi. Z-test on üks statistiliste hüpoteeside testimismeetodite aluseid ja seda õpitakse sageli sissejuhataval tasemel. Mõne aja z-teste saab kasutada ka siis, kui andmed genereeritakse muust jaotusest, näiteks binoom ja Poisson.
Z Testi statistika valemi kalkulaator
Võite kasutada järgmist Z-testi statistika kalkulaatorit
| x̄ | |
| μ | |
| σ | |
| √n | |
| Z test | |
| Z Test = |
|
|
Soovitatavad artiklid
See on olnud Z-testi statistika valemi juhend. Siin käsitleme kuidas arvutada Z-testi statistikat koos praktiliste näidetega. Pakume Z-testi statistika kalkulaatorile ka allalaaditavat Exceli malli. Lisateabe saamiseks võite vaadata ka järgmisi artikleid -
- Mis on hüpergeomeetriline jaotusvalem?
- Hüpoteesi testimise valem | Mõiste | Kalkulaator
- Näited määramiskoefitsiendi valemi kohta
- Kuidas arvutada valemi abil proovi suurust?