
Määramiskoefitsient valemiga (sisukord)
- Valem
- Näited
Mis on määramiskoefitsiendi valem?
Statistikas on määramiskoefitsient, mida nimetatakse ka R 2, tööriist, mis määrab kindlaks ja hindab statistilise mudeli võimet selgitada ja ennustada tulevasi tulemusi. Teisisõnu, kui meil on mudelis sõltuv muutuja y ja sõltumatu muutuja x, siis aitab R2 määrata variatsiooni y variatsiooni x järgi. See on regressioonanalüüsi üks peamisi väljundeid ja seda kasutatakse siis, kui soovime ennustada tulevikku või katsetada mõnda mudelit koos sellega seotud teabega. R2 väärtus jääb vahemikku 0–1 ja suurem on R2 väärtus, seda parem on mudeli ennustus ja tugevus. R 2 on väga sarnane korrelatsioonikordajaga, kuna korrelatsioonikordaja mõõdab kahe muutuja otsest seost. R 2 on põhimõtteliselt korrelatsioonikordaja ruut.
Määramiskoefitsiendi valem:
Määramiskoefitsiendi arvutamiseks on mitu valemit:
- Korrelatsioonikordaja kasutamine:
Correlation Coefficient = Σ ((X – X m ) * (Y – Y m )) / √ (Σ (X – X m ) 2 * Σ (Y – Y m ) 2 )
Kus:
- X - andmepunktid andmekogumis X
- Y - andmepunktid andmekogumis Y
- X m - andmekogu X keskmine
- Y m - andmekogu Y keskmine
Nii
Coefficient of Determination(R 2 ) = (Correlation Coefficient) 2
- Regressiooniväljundite kasutamine
Määramiskoefitsient (R 2 ) = seletatud variatsioon / variatsioon kokku
Määramiskoefitsient (R 2 ) = MSS / TSS
Coefficient of Determination (R 2 ) = (TSS – RSS) / TSS
Kus:
- TSS - ruutude kogusumma = Σ (Yi - Ym) 2
- MSS - ruutude mudelsumma = Σ (Y - Ym) 2
- RSS - ruutude jääksumma = Σ (Yi - Y ^) 2
Y on mudeli ennustatud väärtus, Yi on i-nda väärtus ja Ym on keskmine väärtus
Näited määramiskoefitsiendi valemi kohta (Exceli malliga)
Võtame näite, et mõistmiskoefitsiendi arvutamist paremini mõista.
Selle määramiskoefitsiendi valemi Exceli mall saate alla laadida siit - valemi Exceli määramiskoefitsient.Määramiskoefitsient valemiga - näide # 1
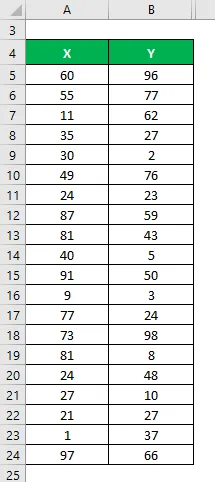
Oletame, et meil on kaks andmekogumit X & Y ja igaüks sisaldab 20 juhuslikku andmepunkti. Arvutage andmekogumi X & Y määramiskoefitsient.
Keskmine arvutatakse järgmiselt:
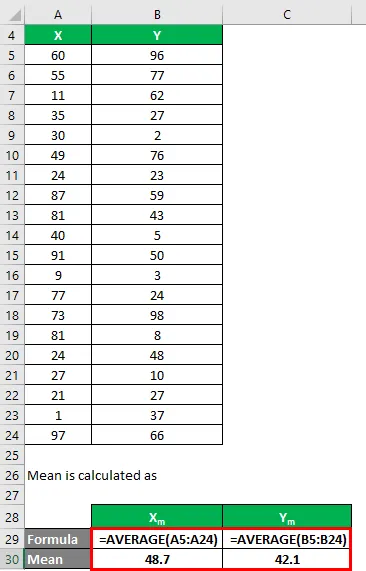
- Andmekogumi keskmine X = 48, 7
- Andmekogumi keskmine Y = 42, 1
Nüüd peame arvutama erinevuse andmepunktide ja keskmise väärtuse vahel.
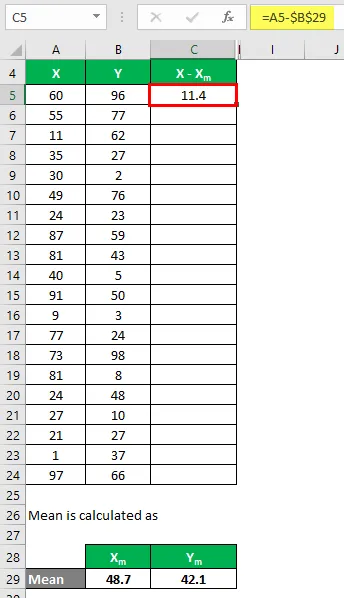
Samamoodi arvutage kõigi X-i andmekogumite jaoks.
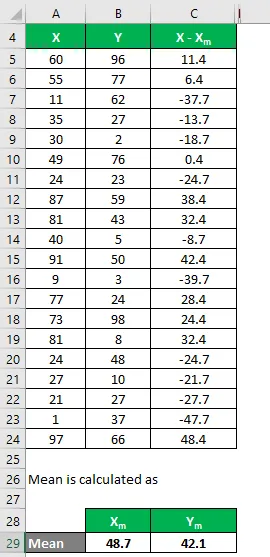
Samamoodi arvutage see ka andmekogumi Y jaoks.

Arvutage erinevuse ruut nii andmekogumite X kui Y jaoks.
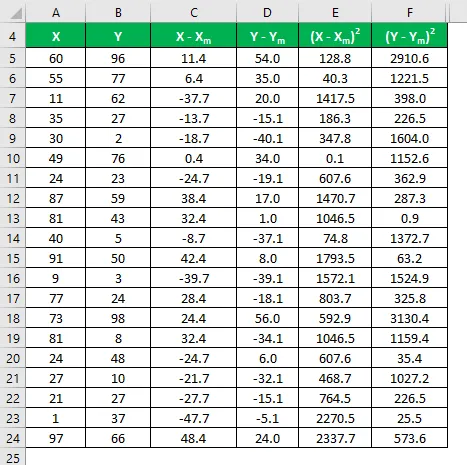
Korrutage X-i erinevus Y-ga.
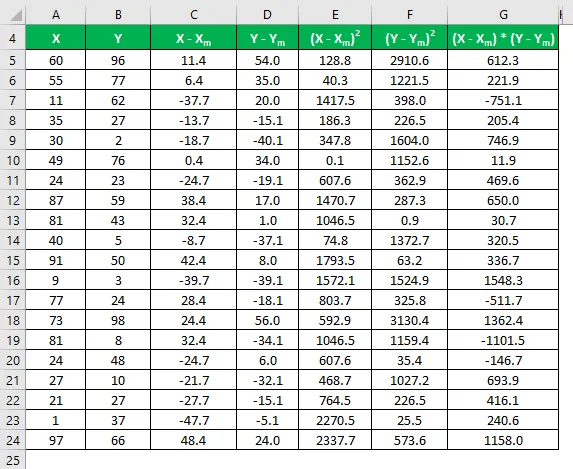
Korrelatsioonikordaja arvutatakse järgmise valemi abil
Korrelatsioonikordaja = Σ ((X - X m ) * (Y - Y m )) / √ (Σ (X - X m ) 2 * Σ (Y - Y m ) 2 )
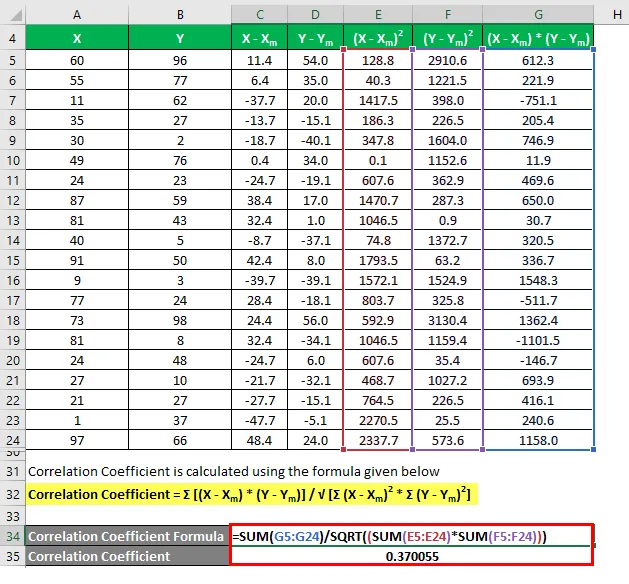
Määramiskoefitsient arvutatakse järgmise valemi abil
Määramiskoefitsient = (korrelatsioonikoefitsient) 2
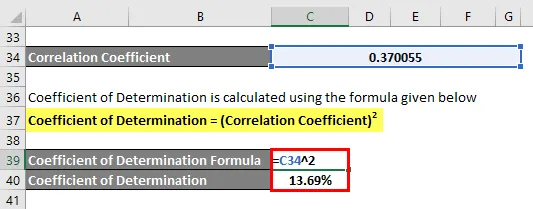
Määramiskoefitsient = 13, 69%
Määramiskoefitsient valemiga - näide # 2
Ütleme, et olete väga riskikartlik investor ja soovite investeerida raha aktsiaturule. Te pole kindel, millistesse aktsiatesse investeerida, ja ka teie riskivalmidus on madal. Nii et soovite investeerida aktsiatesse, mis on ohutud ja mis võivad indeksi toimimist jäljendada. Teie sõber, kes on aktiivne investor, on teie alus- ja tehnilise teabe põhjal valinud teile 3 aktsiat ja soovite nende kolme hulgast valida 2 aktsiat.
Samuti olete kogunud teavet nende viimase 15 aasta ajaloolise tulu kohta.
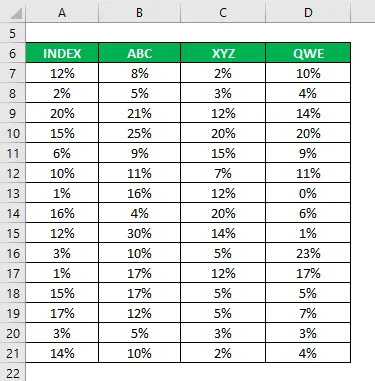
Korrelatsioonikoefitsient arvutatakse exceli valemi abil
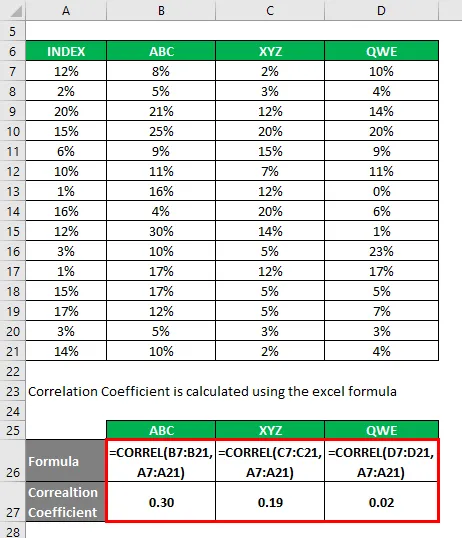
Määramiskoefitsient arvutatakse järgmise valemi abil
Määramiskoefitsient = (korrelatsioonikoefitsient) 2
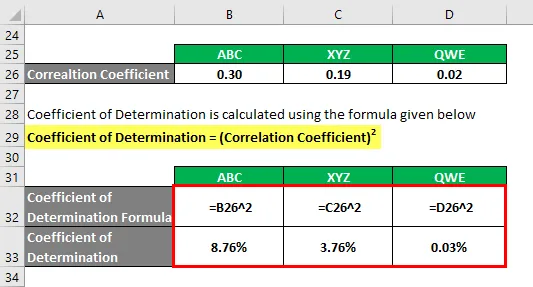
Selle teabe põhjal valite investeerimiseks aktsiad ABC ja XYZ, kuna neil on kõrgeim määramiskoefitsient.
Seletus
Nagu eespool selgitatud, on määramiskoefitsient kahe andmekogumi vahelise korrelatsiooni ruut. Kui R2 on 0, tähendab see, et korrelatsiooni pole ja sõltumatu muutuja ei suuda sõltuva muutuja väärtust ennustada. Samamoodi, kui selle väärtus on 1, tähendab see, et sõltumatu muutuja on alati edukas sõltuva muutuja ennustamisel. Kuid seal on ka mõned piirangud. Ehkki see ütleb meile korrelatsiooni kahe andmekogumi vahel, ei ütle see meile, kas see väärtus on piisav või mitte.
Samuti ei tähenda suur väärtus R 2 alati seda, et kahel muutujal on tugevad seosed ja see võib olla rämps. Näiteks: ütleme, et R 2 väärtus aasta jooksul müüdud autode ja aastas müüdud jäätisekarpide vahel on 80%. Kuid nende kahe vahel pole mingit seost. Seega tuleks R2 kasutamisel olla väga ettevaatlik, kõigepealt aru saada andmetest ja seejärel meetodit rakendada
Määramiskoefitsiendi valemi olulisus ja kasutamine
R2-l on palju praktilisi rakendusi. Näiteks kasutavad investorid R2 väga sageli oma portfelli tootlust turul ja proovivad ennustada ka tulevasi suundi. Sarnaselt aitab riskifondide kasutamine R 2-l neil oma mudelites riski modelleerida. Kuid lõppkokkuvõttes põhineb tulemus puhtal arvul ja statistikal, mis võib mõnikord olla eksitav. Nagu eespool mainitud, tuleb kõigepealt kontrollida, kas R2 väljund on reaalses elus mõttekas või mitte.
Soovitatavad artiklid
See on olnud määramiskoefitsiendi valemi juhend. Siin arutatakse, kuidas arvutada määramiskoefitsient koos praktiliste näidete ja allalaaditava excelimalliga. Lisateabe saamiseks võite vaadata ka järgmisi artikleid -
- Tururiski preemiavalemi juhend
- Katvuse suhte valemi näited
- Tegevuspõhise kuluarvestusvalemi kalkulaator
- Kuidas arvutada valemit kasutades teabesuhet?