
Variatsioonikordaja valem (sisukord)
- Valem
- Näited
Mis on variatsioonikordaja valem?
Statistikas on variatsioonikordaja, mida nimetatakse ka CV-ks, tööriistaks, mis aitab meil kindlaks teha, kuidas andmekogumi andmepunktid jagunevad keskmisena. Põhimõtteliselt joonistatakse kõigepealt kõik andmepunktid ja seejärel kasutatakse variatsioonikordajat, et mõõta nende punktide üksteisest hajumist ja keskmist. Nii aitab see meil andmetest aru saada ja näha ka nende moodustumist. See arvutatakse andmekogumi standardhälbe ja keskmise väärtuse suhtena. Suurem variatsioonikoefitsient tähendab, et andmete hajutatus keskmise ümber on suurem. Sarnaselt, mida madalam on variatsioonikordaja väärtus, seda väiksem on dispersioon ja täpsemad on tulemused. Isegi kui kahe andmerea keskmine on märkimisväärselt erinev, on variatsioonikordaja väga kasulik, et võrrelda varieeruvuse astet ühelt andmeriigilt teisele.
Variatsioonikordaja valem saadakse järgmiselt:
Coefficient of Variation = Standard Deviation / Mean
Variatsioonikoefitsiendi arvutamise sammud:
1. samm: arvutage andmekogumi keskmine. Keskmine on kõigi väärtuste keskmine ja selle saab arvutada kõigi väärtuste summa summeerimisel ja jagades selle arvu andmepunktidega.
2. samm: seejärel arvutage andmekogumi standardhälve. See on vähe aeganõudev protsess. Standardhälvet saab arvutada järgmiselt: √ (Σ (X i - X m ) 2 / (n - 1)) . X i on i-ndaks andmepunktiks ja X m on andmekogumi keskmine. Alternatiivina võime leida standardhälbe ka excelis, kasutades funktsiooni STDEV.S ().
3. samm: Jagage variatsioonikordaja saamiseks standardhälve keskmisega.
Variatsioonikordaja valemi näited (Exceli malliga)
Võtame näite, et variatsioonikordaja arvutamist paremini mõista.
Selle variatsioonikordaja valemi Exceli mall saate alla laadida siit - valemi variatsioonikoefitsient Exceli mallVariatsioonikordaja valem - näide # 1
Oletame, et meil on kaks andmekogumit A ja B ning igaüks sisaldab 20 juhuslikku andmepunkti. Arvutage variatsioonikoefitsient andmekogumile X & Y.
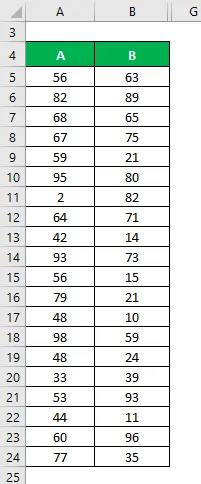
Lahendus:
Keskmine arvutatakse järgmiselt:
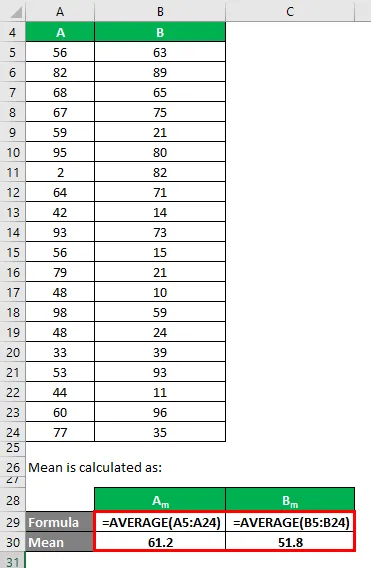
- Andmekogumi keskmine A = 61, 2
- Andmekogumi B keskmine = 51, 8
Nüüd peame arvutama erinevuse andmepunktide ja keskmise väärtuse vahel.
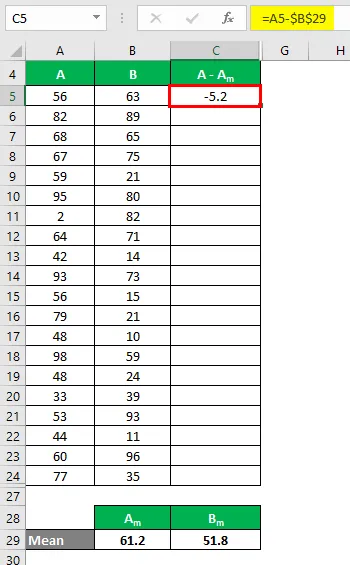
Samamoodi arvutage kõigi andmekogumi A väärtuste jaoks.
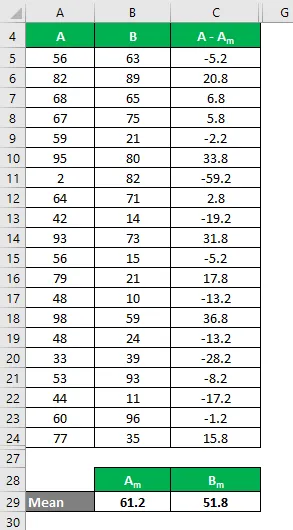
Samamoodi arvutage kõigi andmekogumi B väärtuste jaoks.
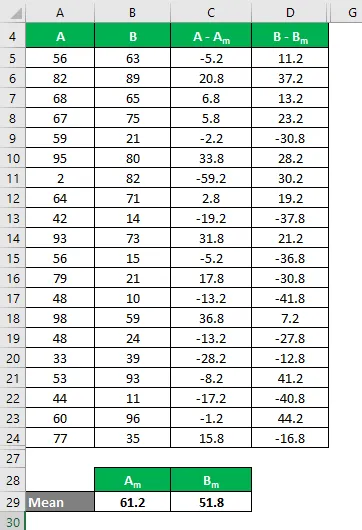
Arvutage erinevuse ruut nii andmekogumite A kui ka B jaoks.
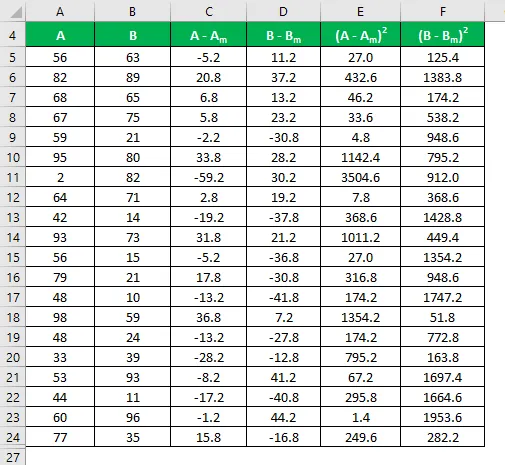
Standardhälve arvutatakse järgmise valemi abil
Standardhälve = √ (Σ (X i - X m ) 2 / (n - 1))
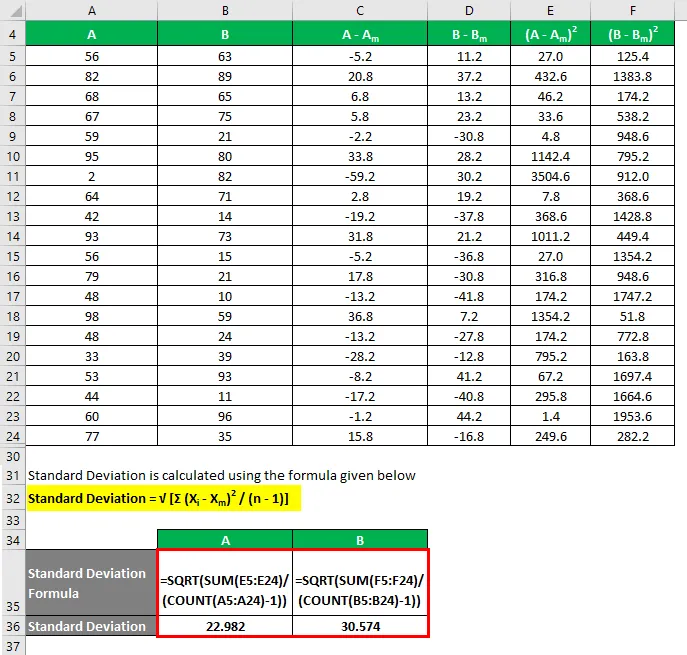
Variatsioonikordaja arvutatakse järgmise valemi abil
Variatsioonikordaja = standardhälve / keskmine
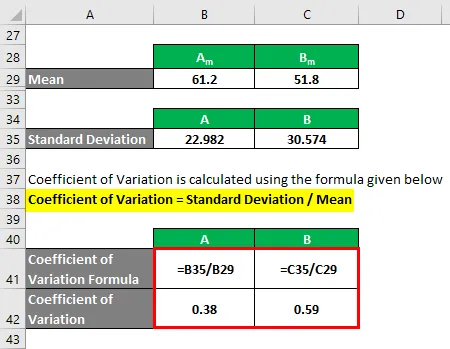
- Variatsioonikordaja A = 22, 982 / 61, 2 = 0, 38
- Variatsioonikoefitsient B = 30, 574 / 51, 8 = 0, 59
Nii et kui näete siin, on B-l suurem variatsioonikoefitsient kui A-l, mis tähendab, et B-i andmepunktid on hajutatumad kui A.
Variatsioonikordaja valem - näide # 2
Ütleme, et olete väga riskikartlik investor ja soovite investeerida raha aktsiaturule. Kuna teie riskivalmidus on madal, soovite investeerida turvalistesse aktsiatesse, millel on madalam standardhälve ja variatsioonikordaja. Olete valinud 3 aktsiat nende põhi- ja tehnilise teabe põhjal ja soovite valida 2 aktsiat. Samuti olete kogunud teavet nende viimase 15 aasta ajaloolise tulu kohta.
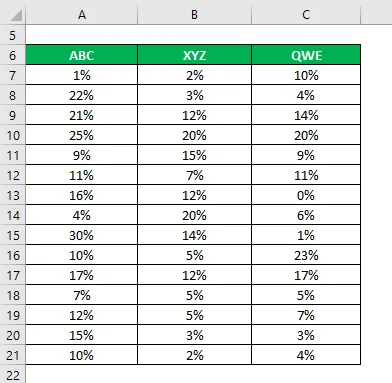
Lahendus:
Keskmine arvutatakse järgmiselt:
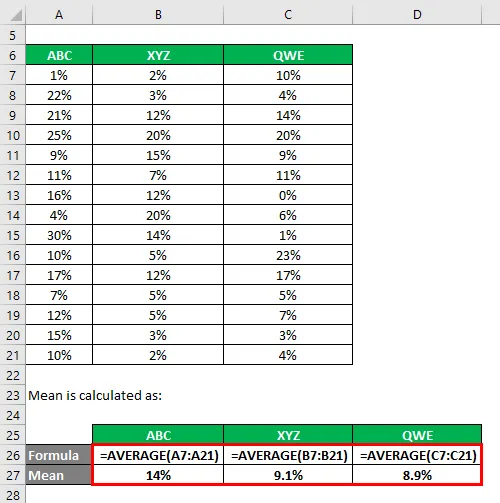
Standardhälbe arvutamiseks kasutatakse exceli valemit
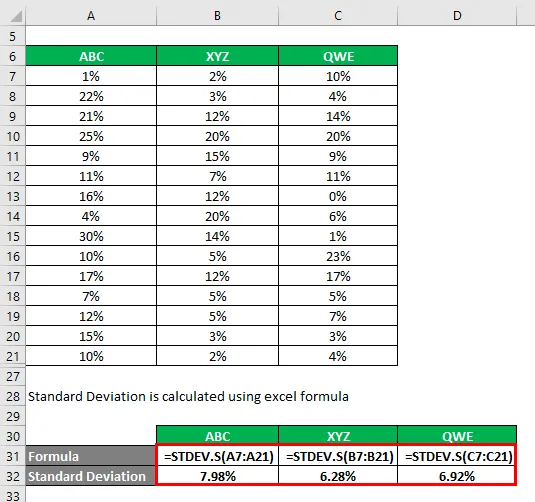
Variatsioonikordaja arvutatakse järgmise valemi abil
Variatsioonikordaja = standardhälve / keskmine
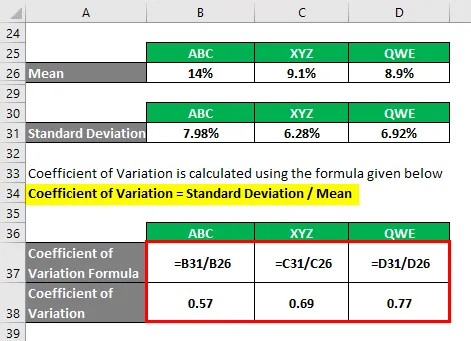
- Variatsioonikordaja ABC = 7, 98% / 14% = 0, 57
- Variatsioonikordaja XYZ = 6, 28% / 9, 1% = 0, 69
- Variatsioonikoefitsient QWE = 6, 92% / 8, 9% = 0, 77
Selle teabe põhjal valite investeerimiseks aktsiad ABC ja XYZ, kuna nende variatsioonikordaja on madalaim.
Seletus
Kuna variatsioonikordaja on riski mõõdik, aitab see mõõta aktsiate ja muude finantsinstrumentide hindade kõikumist. Samuti aitab see investoritel ja analüütikutel võrrelda erinevate võimalike investeeringutega seotud riske.
Variatsioonikoefitsient sarnaneb standardhälbega, kuid kahe muutuja standardhälvet ei saa kasulikkuses võrrelda. Kuid standardhälbe ja keskmise kasutamine muudab suhtelise võrdluse mõttekamaks. Samuti on variatsioonikoefitsient piiratud. Oletame, et selle andmekogumi keskmine on null. Sel juhul muutub see tööriist ebaefektiivseks. Ja mitte ainult, kui meil on andmekogum, millel on palju positiivseid ja negatiivseid väärtusi, muutub variatsioonikordaja väga problemaatiliseks. Seega on see kasulikum ainult siis, kui andmekogumitel on sama pluss-miinus märk.
Variatsioonikordaja valemi olulisus ja kasutamine
Variatsioonikordaja on asjakohane paljudes muudes valdkondades peale statistika. Näiteks rahanduse valdkonnas on variatsioonikordaja riskinäitaja. See sarnaneb standardhälbega, kuna seda kasutatakse ka riskinäitajana, kuid erinevus seisneb selles, et variatsioonikordaja on suhtelise riski parem näitaja. Näiteks oletame, et A eeldatav tootlus on 15% ja B eeldatav tootlus on 10% ning A-l on standardhälve 10%, samal ajal kui B-l on standardhälve 5%. Parema investeeringu valimiseks võib kasutada variatsioonikordajat. Niisiis on A variatsioonikordaja 10/15 = 0, 666 ja B variatsioonikordaja on 5/10 = 0, 5. Seega on B parem investeering kui A.
Soovitatavad artiklid
See on variatsioonikordaja valemi juhend. Siin arutleme, kuidas arvutada variatsioonikordaja valemi abil koos praktiliste näidete ja allalaaditava excelimalliga. Lisateabe saamiseks võite vaadata ka järgmisi artikleid -
- Mis on kohandatud R ruutu valem?
- Näited määramiskoefitsiendi valemi kohta
- Kuidas arvutada valemi abil korrelatsioonikordaja?
- Kovariantsuse valem koos Exceli malliga