
Sissejuhatus hashing-funktsiooni C-s
Selles artiklis on lühike märkus räsimise kohta (räsitabel ja räsifunktsioon). Kõige olulisem mõiste on otsimine, mis määrab aja keerukuse. Aja keerukuse vähendamiseks võetakse kasutusele mis tahes muu andmestruktuuriga räsimise kontseptsioon, millel on keskmisel juhul O (1) aeg ja halvimal juhul võtab see O (n) aega.
Rähistamine on tehnika kiirema juurdepääsuga elementidele, mis kaardistab antud andmed võrdluseks väiksema võtmega. Üldiselt jälgitakse selles tehnikas klahve räsifunktsiooni abil tabelisse, mida tuntakse räsitabelina.
Mis on räsifunktsioon?
Räsifunktsioon on funktsioon, mis kasutab väärtuste salvestamiseks ja leidmiseks räsitabelist konstantse tööajaga toimingut, mida rakendatakse võtmetele täisarvudena ja seda kasutatakse räsitabeli väärtuste aadressina.
Räsifunktsiooni tüübid
Räsifunktsioonide tüüpe selgitatakse allpool:
1. Jagunemismeetod
Selle meetodi puhul sõltub räsifunktsioon ülejäänud jagunemisest.
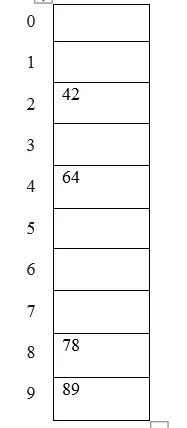
Näide: räsitabelisse paigutatavad elemendid on 42, 78, 89, 64 ja võtkem tabeli suuruseks 10.
Hash (võti) = elemendid% tabeli suurusest;
2 = 42% 10;
8 = 78% 10;
9 = 89% 10;
4 = 64% 10;
Tabeli esitust saab vaadata järgmiselt:
2. Keskmise ruudu meetod
Selle meetodi puhul võetakse indeksiks ruudu elemendi keskmine osa.
Räsitabelisse paigutatav element on 210, 350, 99, 890 ja laua suurus 100.
210 * 210 = 44100, indeks = 1, kuna tulemuse (44100) keskmine osa on 1.
350 * 350 = 122500, indeks = 25, kuna tulemuse (122500) keskmine osa on 25.
99 * 99 = 9801, indeks = 80, kuna tulemuse (9801) keskmine osa on 80.
890 * 890 = 792100, indeks = 21, kuna tulemuse (792100) keskmine osa on 21.
3. Digitaalse voltimise meetod
Selle meetodi puhul on tabelisse paigutatav element sing hash-võti, mis saadakse, jagades elemendid erinevateks osadeks ja ühendades seejärel osad lihtsate matemaatiliste toimingutega.
Asetatav element on 23576623, 34687734.
- räsi (võti) = 235 + 766 + 23 = 1024
- räsiklahv) = 34 + 68 + 77 + 34 = 213
Oletame, et seda tüüpi räsimise korral on arvud vahemikus 1 kuni 100 ja räsitabeli suurus = 10. Elemendid = 23, 12, 32
Hash (võti) = 23% 10 = 3;
Hash (võti) = 12% 10 = 2;
Hash (võti) = 32% 10 = 2;
Ülaltoodud näite põhjal pange tähele, et mõlemad elemendid 12 ja 32 osutavad tabeli 2. kohale, kus pole võimalik kirjutada mõlemaid samasse kohta. Sellist probleemi nimetatakse kokkupõrkeks. Selliste probleemide vältimiseks on mõned räsifunktsioonide tehnikad, mida saab kasutada.
Kokkupõrke lahendamise tehnikate tüübid
Arutleme kokkupõrke lahendamise tehnikatüüpide üle:
1. Aheldamine
Selle meetodi puhul, nagu nimigi ütleb, pakub see tabeli kirje kastide ahela, millel on kaks elemendi kirjet. Nii et kui sellised kokkupõrked toimuvad, moodustuvad lahtrid lingitud loendina.
Näide: 23, 12, 32 laua suurusega 10.
Hash (võti) = 23% 10 = 3;
Hash (võti) = 12% 10 = 2;
Hash (võti) = 32% 10 = 2;
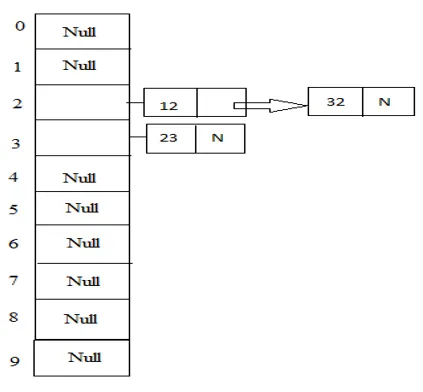
2. Avage Adresseerimine
- Lineaarne sond
See on veel üks meetod kokkupõrkeprobleemide lahendamiseks. Nagu nimi ütleb, kui toimub kokkupõrge, tuleks tabeli samale kirjele paigutada kaks elementi, kuid selle meetodi abil saame otsida tabelist järgmise tühja ruumi või kirje ja asetada teine element. See võib jälle viia uue probleemini; kui me ei leia tabelist ühtegi tühja kirjet, siis viib see klastritesse. Seega tuntakse seda klasterdamisprobleemina, mida saab lahendada järgmise meetodiga.
Näide: 23, 12, 32 laua suurusega 10
Hash (võti) = 23% 10 = 3;
Hash (võti) = 12% 10 = 2;
Hash (võti) = 32% 10 = 2;

Sellel diagrammil saab 12 ja 32 paigutada indeksiga 2 samasse sisestusse, kuid selle meetodi abil paigutatakse need lineaarselt.
- Ruutmeetriline sondimine
See meetod on lahendus klasterdamisprobleemile lineaarsel sondimisel. Selle meetodi korral arvutatakse räsi võtmega räsifunktsioon järgmiselt: räsi (võti) = (räsi (võti) + x * x)% tabeli suurusest (kus x = 0, 1, 2…).
Näide: 23, 12, 32 laua suurusega 10
Hash (võti) = 23% 10 = 3;
Hash (võti) = 12% 10 = 2;
Hash (võti) = 32% 10 = 2;

Selles näeme, et 23 ja 12 saab hõlpsalt paigutada, kuid 32 ei saa jällegi 12 ja 32 jagada sama kannet sama indeksiga tabelis, kuna selle meetodi puhul räs (võti) = (32 + 1 * 1) % 10 = 3. Kuid sel juhul on tabeli kirje indeksiga 3 paigutatud 23-ga, nii et me peame x väärtust suurendama ühe võrra. Rõhulülitus (võti) = (32 + 2 * 2)% 10 = 6. Nii saame nüüd paigutada 32 kandes tabelis indeksiga 6.
- Topelt räsimine
Selle meetodi abil peame arvutama 2 räsifunktsiooni, et lahendada kokkupõrkeprobleem. Esimene arvutatakse lihtsa jagamismeetodi abil. Teiseks peab vastama kahele reeglile; see ei tohi olla võrdne nulliga ja kandeid tuleb mõõta.
- 1 (võti) = klahvi% tabeli suurus.
- 2 (klahv) = p - (klahv mod p), kus p on algarvud <tabeli suurus.
Näide: 23, 12, 32 laua suurusega 10
Hash (võti) = 23% 10 = 3;
Hash (võti) = 12% 10 = 2;
Hash (võti) = 32% 10 = 2;
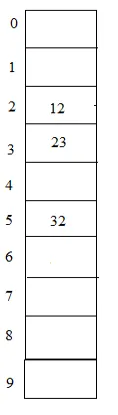
Selles saab elemendi 32 uuesti paigutada, kasutades hash2 (võti) = 5 - (32% 5) = 3. Seega saab 32 paigutada tühja tabeli viitenumbri 5 juurde, kuna selle paigutamiseks peame hüppama 3 kirjet.
Järeldus-räsimisfunktsioon C-s
Räsimine on üks olulisi tehnikaid andmete otsimisel, pakkudes väga tõhusaid ja kiireid meetodeid, kasutades räsifunktsiooni ja räsitabeleid. Iga elementi saab otsida ja paigutada erinevate räsimeetodite abil. See meetod on ajakoefitsiendi osas väga kiirem kui ükski teine andmestruktuur.
Soovitatavad artiklid
See on juhend C-põhise räsimise funktsioonist. Siin käsitleme lõiku C funktsiooni rühmitamist, mis on räsifunktsioon, räsifunktsiooni tüübid jne. Lisateabe saamiseks võite tutvuda ka meie teiste soovitatud artiklitega -
- Räsimine DBMS-is
- Krüptimisprotsess
- Kuidas installida CakePHP?
- Kuidas plokiahel töötab?
- Räsimisfunktsioon Java-s
- Räsimisfunktsioon PHP-s | Kuidas töötada?