Hierarhiline klasterdamisalgoritm - Hierarhilise klastrimise tüübid ja sammud

Lang L: none (table-of-contents):

Anonim

Sissejuhatus hierarhilisse klasterdamisalgoritmi

Hierarhiline rühmituse algoritm on juhendamata masinõppe tehnika. Selle eesmärk on leida andmete omaduste põhjal loomulik rühmitus.

Hierarhilise rühmitamise algoritmi eesmärk on hierarhia ülesehitamise abil leida andmete pesastatud rühmad. See sarnaneb taime- või loomariigi bioloogilise taksonoomiaga. Hierarhilised klastrid on tavaliselt esindatud dendrogrammina tuntud hierarhilise puu abil.

Hierarhilise klasterdamisalgoritmi tüübid

Hierarhilisi rühmitamise algoritme on kahte tüüpi:

  • Jagav
  • Aglomeratiivne

1. Jagav

See on ülalt alla lähenemisviis, kus ta algselt arvestab kogu andmeid ühe rühmana ja jagab seejärel andmed iteratiivselt alarühmadesse. Kui hierarhilise klasterdamisalgoritmi arv on teada, siis jagunemisprotsess peatub, kui klastrite arv on saavutatud. Muus osas protsess peatub, kui andmeid ei saa enam jagada, mis tähendab, et praegusest iteratsioonist saadud alarühm on sama, mis eelmisest iteratsioonist saadud (võib arvestada ka sellega, et jagunemine peatub, kui iga andmepunkt on klaster) ).

2. Aglomeratiivne

See on alt üles suunatud lähenemisviis, mis tugineb klastrite liitmisele. Esialgu jaotatakse andmed m üksikuteks klastriteks (kus m väärtus on proovide / andmepunktide arv). Kaks klastrit liidetakse iteratiivselt üheks, vähendades klastrite arvu igas iteratsioonis. See klastrite liitmise protsess peatub, kui kõik klastrid on liidetud ühte või kui soovitud klastrite arv on saavutatud.

1. tasemel on m klastrit, mis taandub tasemel 1 m klastriks. Need andmepunktid, mis liidetakse madalamal tasemel klastriks, jäävad samasse klastrisse ka kõrgematel tasemetel. Näiteks oletame, et punkte 8 on x1..x8, nii et algselt on tasemel 1 klastrit. Oletame, et punktid x1 ja x2 liidetakse klastriks 2. tasemel, siis kuni tasemeni 8 jäävad nad samasse klastrisse.

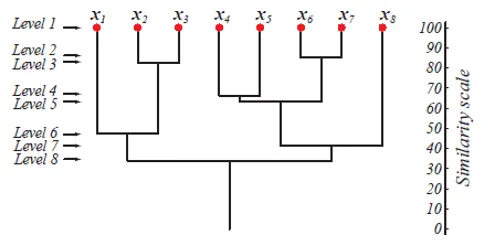
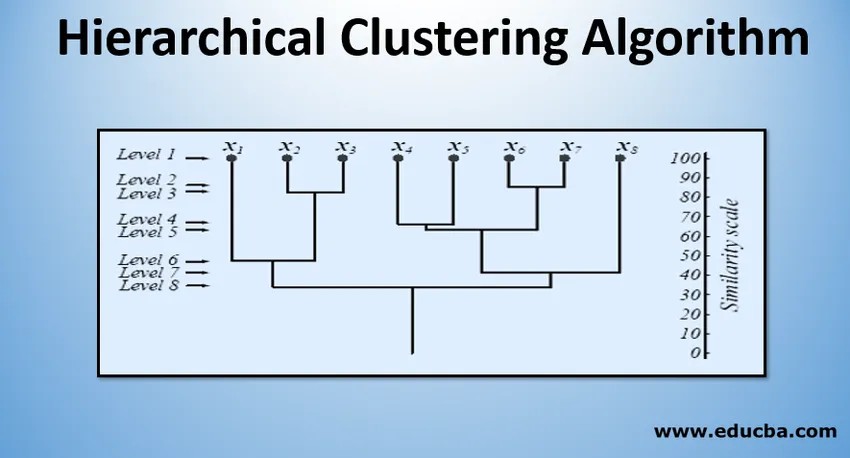
Ülaltoodud joonis näitab 8 andmepunkti aglomeratsiooni rühmitamise lähenemisviisi dendrogrammina ja igale tasemele vastavat sarnasusskaalat.

Klastrite tasemed annavad meile ettekujutuse klastrite andmepunktide sarnasusest. Nagu joonisel 1 näidatud, liidetakse andmepunktid varem klastriks, sarnased nad on. Niisiis, klastri 2. taseme andmepunktid (nt x2 ja x3) on sarnasemad kui klastri 6. taseme andmepunktid (nt x1 ja x2).

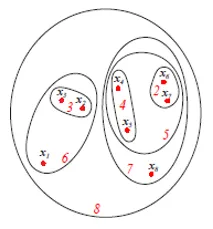
Ülaltoodud joonis näitab ülalnimetatud 8 andmepunkti aglomeratiivse rühmitamise lähenemisviisi diagrammi Set või Venn diagrammi. Klastrimiseks saab kasutada nii dendrogramme kui ka komplekti esindusi. Kuid tavaliselt on eelistatav dendrogramm. Vara esitus ei saa kvantitatiivselt kajastada klastri sarnasusi.

Hierarhilise klasterdamisalgoritmi sammud

Järgigem allpool toodud hierarhilise rühmitamise algoritmi jaoks järgmisi samme:

1. Algoritm

Aglomeratiivne hierarhiline rühmitamise algoritm

  1. Alustage initsialiseerimist c, c1 = n, Di = (xi), i = 1, …, n '
  2. Tehke c1 = c1 - 1
  3. Leidke lähimad klastrid, näiteks Di ja Dj
  4. Ühenda Di ja Dj
  5. Kuni c = c1
  6. Tagastage c klastrid
  7. Lõpp

See algoritm algab n klastriga, kus iga andmepunkt on klaster. Iga iteratsiooniga väheneb klastrite arv ühe võrra, kui 2 lähimat klastrit ühinevad. Seda protsessi jätkatakse seni, kuni klastrite arv väheneb etteantud väärtuseni c.

Kuidas otsustada, millised klastrid on lähedal?

Seda määratletakse mitmete järgmiste kaugusmõõdikute abil:

  • Klastrite vaheline minimaalne kaugus dmin (Di, Dj). Kasulik üksikute jaoks.
  • Maksimaalne vahemaa klastrite vahel dmax (Di, Dj). Kasulik täielik.
  • Keskmine klastrite vaheline kaugus davg (Di, Dj).

Mis on ühekordne ja täielik ühendus?

  • Kui kahe klastri vahelise kauguse leidmiseks kasutatakse dmin (di, dj) ja algoritm lõpeb, kui lähimate klastrite vaheline kaugus ületab läve, siis nimetatakse algoritmi ühe seose algoritmiks.
  • Kui kahe klastri vahelise kauguse leidmiseks kasutatakse dmax (Di, Dj) ja algoritm lõpeb, kui lähimate klastrite vaheline kaugus ületab läve, nimetatakse algoritmi täielikuks ühendamise algoritmiks.
  • Vaatleme iga andmepunkti graafiku sõlmena. Kahe andmepunkti vahel on serv, kui need kuuluvad samasse klastrisse. Kui kaks lähimat klastrit on ühendatud, lisatakse serv. Seda nimetatakse üksiksidemeks, kuna ühelt sõlmelt teisele on olemas ainulaadne tee.
  • Täielik ühendamise algoritm ühendab kaks klastrit, minimeerides kahe kaugeima punkti vahelise vahemaa.
  • Üksiku seose algoritm genereerib katva puu. See algoritm on aga müratundlik. Tervikliku ühendamise algoritm loob täieliku graafiku.

Milline on algoritmi ajaline keerukus?

Oletame, et d-mõõtmelises ruumis on n mustrit ja c-klastrite moodustamiseks kasutame dmin (Di, Dj). Peame arvutama n (n - 1) punktide vahekaugused - millest igaüks on O (d 2 ) arvutus - ja paigutama tulemused punktidevahelise vahemaa tabelisse. Ruumi keerukus on O (n 2 ). Minimaalse vahemaa paari leidmiseks (esimese liitmise jaoks) tuleb läbida täielik nimekiri, hoides väikseima vahemaa indeksit.

Seega on esimese aglomeratiivse etapi keerukus O (n (n - 1) (d2 + 1)) = O (n 2 d2). Teise suvalise aglomeratsiooni etapi jaoks (st vahemikust c1 kuni c1 - 1) astume lihtsalt läbi n (n - 1) - c1 "kasutamata" vahemaad loendis ja leiame väikseima, mille jaoks x ja x 'asuvad erinevates klastrites . See on jällegi O (n (n − 1) − c1). Kogu ajaline keerukus on seega O (cn 2 d 2 ) ja tüüpilistes tingimustes n >> c.

2. Visualiseerimine

Kui andmed on klastriteks jagatud, on hea tava klastrid visualiseerida, et saada aimu, kuidas rühmitus välja näeb. Kuid selle suure mõõtmega andmete visualiseerimine on keeruline. Seetõttu kasutame visualiseerimiseks põhikomponentide analüüsi (PCA). Pärast PCA-d saame madalmõõtmelises ruumis (tavaliselt 2D või 3D) andmepunktid, mida saame rühmituse nägemiseks joonistada.

Märkus: suur mõõde tähendab suurt hulka funktsioone, mitte arvukalt andmepunkte.

3. Hindamine

Üks klastrite hindamise meetodeid on see, et klastrite vaheline punktide vahe (klastritevaheline kaugus) peaks olema palju suurem kui klastri punktide vaheline kaugus (klastri sisemine kaugus).

Järeldus

Järgnevalt on toodud mõned peamised kaasavõtmised:

  1. Andmetes pesastatud mustrite leidmiseks kasutatakse hierarhilist rühmitamise algoritmi
  2. Hierarhilist rühmitust on kahte tüüpi - lõhestav ja aglomeratiivne
  3. Esindamiseks saab kasutada dendrogrammi ja set / Venni diagrammi
  4. Üksikühendus ühendab kaks klastrit, minimeerides nendevahelise minimaalse vahemaa. See moodustab laiaulatusliku
  5. Täielik ühendus ühendab kaks klastrit, minimeerides maksimaalse vahemaa. See moodustab täieliku graafiku.
  6. Hierarhilise klasterdamisalgoritmi koguaegne keerukus on O (cn 2 d 2 ), kus c on klastrite etteantud arv, n on mustrite arv ja d on n mustri d-mõõtmeline ruum.

Soovitatavad artiklid

See on juhend Hierarhilise klastri algoritmi juurde. Siin käsitleme hierarhiliste rühmitamise algoritmide tüüpe ja samme. Lisateabe saamiseks võite vaadata ka järgmisi artikleid -

  1. Hierarhiline klastrianalüüs
  2. Hierarhiline rühmitus R '-is
  3. Klasterdamisalgoritm
  4. Mis on klastrimine andmete kaevandamisel?
  5. Hierarhiline rühmitus | Aglomeratiivne ja lõhestav klasterdamine
  6. C ++ algoritm | C ++ algoritmi näited