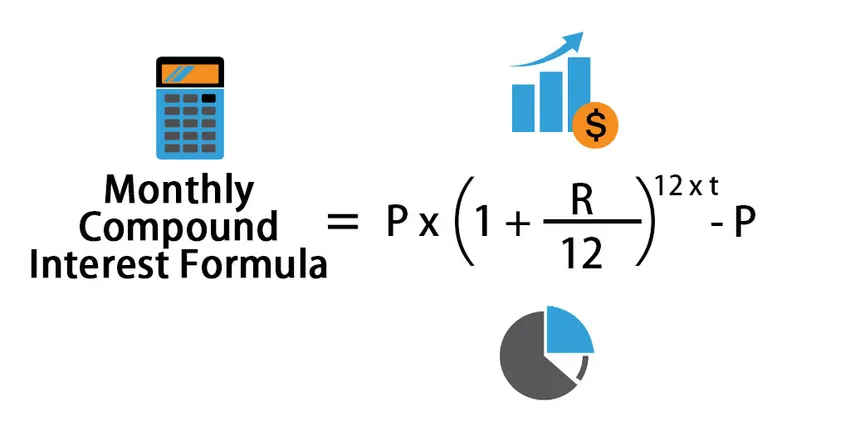
Kuu liitintressi valem - Näited Exceli malliga

Kuu liitintressi valem (sisukord)

• Valem
• Näited
• Kalkulaator

Mis on kuu liitintressi valem?

Kui kindlaks ajaks laenatakse teatud rahasumma ja lisaks laenatud summale tuleb maksta ka täiendav summa. Siis nimetatakse intressiks täiendavat summat, mille maksame fikseeritud määraga. Liitintress on koguintress, mis sisaldab algset intressi ja uue põhiosa intressi, mis kujuneb välja algse põhiosa lisamisega nõuetekohasele intressile. Kuu liidetud arvutamiseks intress, mis liidetakse terve kuu peale kogu aasta jooksul.

Kuu liidetud intressivalemit saab arvutada järgmiselt:

Monthly Compound Interest Formula = P * (1 + (R /12)) 12*t – P

kus,

• P = põhisumma
• R = määr
• t = aeg

Kuu liitintressi valemi näited (Exceli malliga)

Võtame näite, et mõista kuu liitintressi arvutamist paremini.

Selle igakuise liitintressi valemi Exceli malli saate alla laadida siit - Kuu liitintressi valemi Exceli mall

Kuu liitintressi valem - näide nr 1

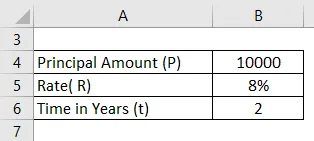
Laenusaaja võttis laenu summas 10 000 Rs intressimääraga 8%. Kas arvutate kuu liit liitintressi 2 aasta kohta?

Lahendus:

Kuu liitintress arvutatakse järgmise valemi abil

Kuu liitintress = P * (1 + (R / 12)) ^{12 * t} - P

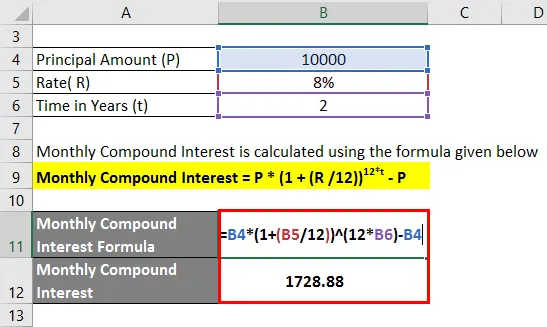
• Kuu liitintress = 10 000 (1 + (8/12)) ^{2 * 12} - 10 000
• Kuu liitintress = 1 728, 88

Kuu liitintress 2 aastat on Rs 1 728, 88

Kuu liitintressi valem - näide nr 2

Investeeritakse rahasumma 10% määraga, mis on 20 000 Rs. Milline on igakuine liitintress 10 aasta jooksul?

Lahendus:

Kuu liitintress arvutatakse järgmise valemi abil

Kuu liitintress = P * (1 + (R / 12)) ^{12 * t} - P

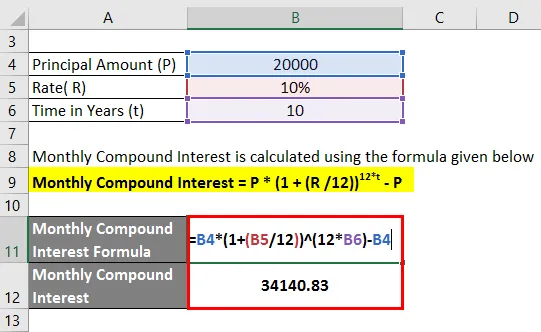
• Kuu liitintress = 20 000 (1 + 10/12)) ^{10 * 12} - 20 000
• Kuu liitintress = 34 140, 83

Kuu liidetud intress 10 aasta eest on Rs 34, 140, 83

Kuu liitintressi valem - näide nr 3

Proua Jefferson ostis antiigi staatuse 500 dollari eest. Viis aastat hiljem müüs ta selle staatuse 800 dollari eest. Ta pidas seda investeeringu osaks. Arvuta tema saadud aastane määr?

Lahendus:

Kui arvestame investeeringuga 500 dollarit ja saame tulevikus 800 000 dollarit, kui t = 10 aastat. Eeldame aastamäära m = 1 ja rakendame selle valemisse.

A = P (1 + r / m) ^mt

• 800 = 500 (1+ r / 1) ^{1 * 10}
• 800 = 500 (1 + r) ¹⁰

Nüüd lahendame määra (r) järgmistes sammudes.

• 800 = 500 (1 + r) ¹⁰
• 8/5 = (1 + r) ¹⁰

Nüüd võtame võrrandi vasakpoolsel küljel jõu (1/10) ja eemaldame paremalt küljelt.

• (8/5) ^1/10) = 1 + r

Arvutage vasakul olev väärtus ja lahendage r.

• 1, 0481 = 1 + r
• 1, 0481 - 1 = r
• 0, 0481 = r

Kuid proua Jefferson teenis aastane intressimäär 4, 81%, mis ei ole halb tootlus.

Seletus

Liitintress on korrutatud algse põhisumma korrutisega, millele lisandub aastane intressimäär, mis tõstetakse liitunud perioodide arvuga miinus üks. Seega lahutatakse saadud väärtusest laenu algsumma.

Liitintressi saab arvutada näiteks:

Liitintressi valem = (P (1 + i) ⁿ ) - P

Liitintressi valem = (P (1 + i) ⁿ - 1)

Kus:

• P = põhisumma
• i = aastane intressimäär protsentides
• n = liitperioodid

On olemas teatud protseduurikomplekt, mille abil saame arvutada kuu liidetud intressi.

1. samm: peame arvutama saadud intressisumma, kasutades igakuist liitintressi. Valemi saab arvutada järgmiselt:

• A = (P (1 + i) ⁿ - 1) - P

2. samm: kui eeldada, et intressimäär on 5% aastas. Kõigepealt peame intressimäära väärtuse väljendama ekvivalentses koma. Seda saab teha järgmisel viisil.

• 5% = 5/100 = 0, 05

3. samm: kuna me teame, et intressi liidetakse igakuiselt, siis võime võtta n = 12. Kuid sel juhul on ajavahemik täpsustatud, võiksime kaaluda, et laen võetakse üheks aastaks. Nüüd on meil olemas kõik muutujad, mida saame otse valemisse asendada ja sellest tulemuse saada.

• A = 1000 ((1 + 0, 05 / 12) ^12–1 )
• A = 1000 ((1 + 0, 0042) ¹² - 1)
• A = 1000 ((1, 0042) 12–1)
• A = 1000 (1, 0516-1)
• A = 1000 (0, 0516)
• A = 51, 6

Oleme ühe kuu intressimäära igakuise liitmise teel arvutanud umbes 51, 6

Kuu liitintress ei kajasta märgatavaid muutusi, kui pargime teatud rahasumma lühiajaliseks. Põhjus on see, et märgatavate muudatuste jõustumiseks võtab kompositsioon mitu aastat.

Ja liitintressi juures on kõige silmatorkavam see, et see paneb teie investeeringud kiiremini kasvama kui lihtsad intressid. Mida tihedam on teie liitmisintervall, seda suurem on erinevus või võime öelda, et igapäevane liitintress teenib teie investeeringutelt rohkem tulu kui iga antud intressimäära aastane liitintress.

Järgmine tabel näitab erinevust, et liitperioodide arv võib teatud aja jooksul teha 10 000 dollari suuruse laenu korral, mille aastane intressimäär on 10% 12-aastase perioodi jooksul.

Liitsagedus	Liitperioodide arv	I ja n väärtused	Intress kokku
Aastas	1	I = 10%, n = 12	21 384, 2837 dollarit
Poolaastas	2	I = 5%, n = 24	22 250 999 USD
Kord kvartalis	4	I = 2, 5%, n = 48	22 714, 8956 dollarit
Igakuine	12	I = 0, 833%, n = 144	23 036, 4896 dollarit

Kuu liitintressi valemi asjakohasus ja kasutamine

Liitintressid on osutunud paremaks investeerimisvahendiks, kuid see võib teie laenusumma suhtes olla väga ohtlik. Lõpuks maksate oma laenusummalt rohkem intressi.

Liitmine muutub efektiivsemaks, kui teie investeering tehakse kas kuu või kvartali asemel, mitte ühe aasta kaupa, kuna see annab parema tulu. Kui laenate raha ükskõik millisest pangast või finantseerimisasutusest, on parim lahendus iga-aastane liitmine. Kindla rahasumma laenutamisel on igapäevane liitmine produktiivsem. Kuid me peaksime meeles pidama, et liit võib sõltuvalt asjaoludest olla nii soodne kui ka ebasoodne.

Liitintress annab teie investeeringult parema tulu, sõltub investeeringu tähtajast ja suurusest. Liitintress kasvab teie ootustest kiiremini.

Liitintressi eelised on loetletud allpool:

1. Reinvesteerimine
2. Parem investeeringutasuvus.
3. Pikaajaline kokkuhoid.
4. Suurenenud tulud.

Kuu liitintressi valemi kalkulaator

Võite kasutada järgmist igakuist liitintressi valemi kalkulaatorit

Lk
R
t
Kuu liitintressi valem

Kuu liitintressi valem =	P x ((1 + R / 12) 12 * t - P)
=	0 x ((1 +0/12) 12 * 0 - 0) = 0

Soovitatavad artiklid

See on kuu liitintresside valemi juhend. Siin arutletakse, kuidas arvutada kuuintressi valemi koos praktiliste näidetega. Pakume ka igakuist liitintressi kalkulaatorit koos allalaaditava excelimalliga. Lisateabe saamiseks võite vaadata ka järgmisi artikleid -

1. Aastase liitkasvu määra valem
2. Kuidas arvutada nominaalset intressimäära?
3. Igapäevane liitintressi valem
4. Poissoni turustusvalemi juhend
5. Intress vs dividend | 8 parimat peamist erinevust, mida peaksite teadma