
Kvartiili kõrvalekalde valem (sisukord)
- Valem
- Näited
- Kalkulaator
Mis on kvartiilhälbe valem?
Kvartili hälve (QD) on ülemise ja alumise kvartiili erinevuse poole korrutis. Matemaatiliselt võime määratleda järgmiselt:
Quartile Deviation = (Q 3 – Q 1 ) / 2
Kvartili hälve määratleb dispersiooni absoluutse mõõtme. QD-le vastavat suhtelist suurust nimetatakse QD koefitsiendiks, mis saadakse valemi teatud komplekti rakendamisel:
Coefficient of Quartile Deviation = (Q 3 – Q 1 ) / (Q 3 + Q 1 )
QD koefitsienti kasutatakse erinevates olukordades varieerumise astme uurimiseks ja võrdlemiseks.
Kvartiilhälbe valemi näited (Exceli malliga)
Võtame näite, et kvartali hälbe valemi arvutamisest paremini aru saada.
Selle kvartiilse kõrvalekalde valemi Exceli mall saate alla laadida siit - kvartiili kõrvalekalde valemi Exceli mallKvartiili kõrvalekalde valem - näide nr 1
Järgmise 10 päeva kohta arvutati sõidukite varastamise kohta päevas esitatud kaebuste arv. Ja andmed on toodud allpool. Arvutage kvartaalse hälve ja selle koefitsient antud diskreetse jaotuse korral.
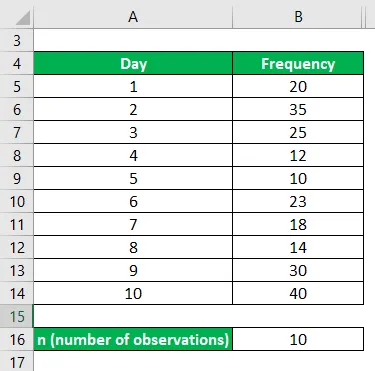
Lahendus:
Andmete järjestamine kasvavas järjekorras
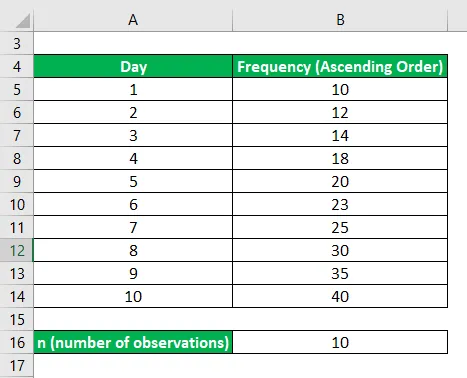
Nüüd leiame esimese kvartiili, nii et see jääb poole väikseima väärtuse ja mediaani vahele; kus kolmas kvartiil asub mediaani ja suurima väärtuse vahel.
Esimene kvartiil (Q 1 ) arvutatakse järgmise valemi abil
Esimene kvartiil ( 1. kvartal)
Q i = (i * (n + 1) / 4) kolmas vaatlus
Q1 = (1 * (10 + 1) / 4) th vaatlus
Q1 = (1 * (10 + 1) / 4) th vaatlus
Q 1 = 2, 75 vaatlus
Niisiis, 2..75 vaatlus asub järjestatud rühmas teise ja kolmanda väärtuse vahel või keskpaigas vahemikus 12–14
Esimene kvartiil (Q 1 ) arvutatakse järgmiselt:
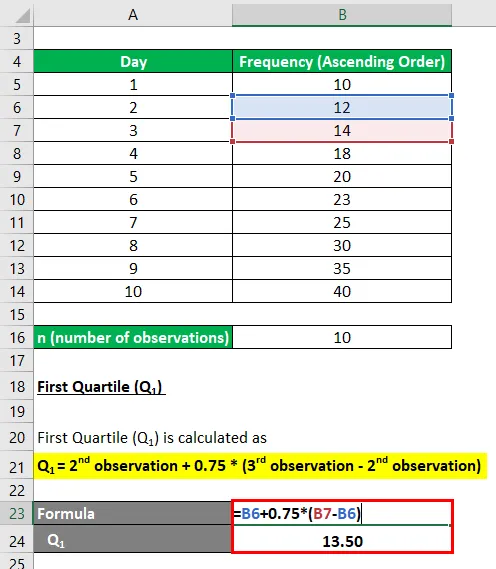
- Q 1 = teine vaatlus + 0, 75 * (kolmas vaatlus - teine vaatlus)
- K 1 = 12 + 0, 75 * (14–12)
- Q 1 = 12 + 1, 50
- Q 1 = 13, 50
Kolmas kvartiil (Q 3 ) arvutatakse järgmise valemi abil
Kolmas kvartiil (Q 3 )
Q i = (i * (n + 1) / 4) th obstruktsioon
- Q 3 = (1 * (n + 1) / 4) th obstruktsioon
- Q3 = ((10 + 1) / 4) th obstruktsioon
- Q 3 = 8, 25 vaatlus
Niisiis, 8.-25 . Vaatlus jääb järjestatud rühmas 8. ja 9. väärtuse vahele või keskpaigas vahemikku 30. – 35.
Kolmas kvartiil (Q 3 ) arvutatakse järgmiselt:
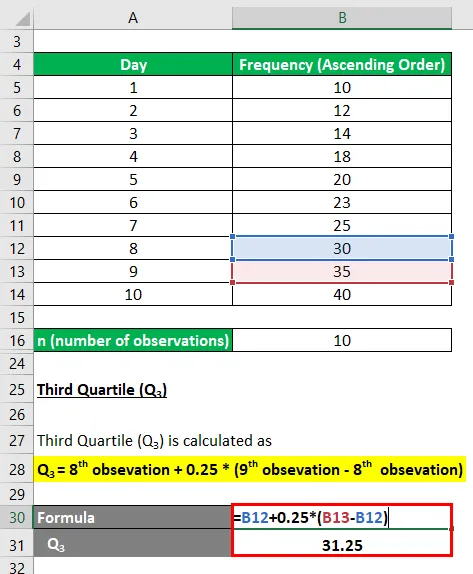
- Q 3 = 8. obsevatsioon + 0, 25 * (9. obsevatsioon - 8. obsevatsioon)
- Q3 = 30 + 0, 25 * (35–30)
- Q 3 = 31, 25
Nüüd kasutades kvartiili väärtusi Q1 ja Q3, arvutame selle kvartiili hälbe ja koefitsiendi järgmiselt -
Kvartiili kõrvalekalle arvutatakse järgmise valemi abil
Kvartiili hälve = (Q 3 - Q 1 ) / 2
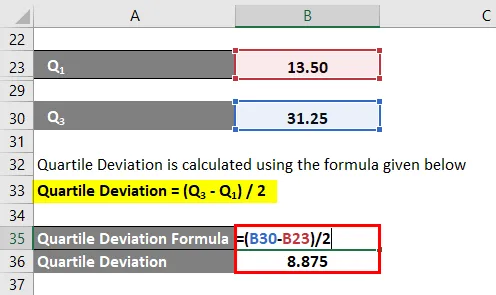
- Kvartiili kõrvalekalle = (31, 25 - 13, 50) / 2
- Kvartiili hälve = 8, 875
Kvartiili kõrvalekalde koefitsient arvutatakse järgmise valemi abil
Kvartiili kõrvalekalde koefitsient = (Q 3 - Q 1 ) / (Q 3 + Q 1 )
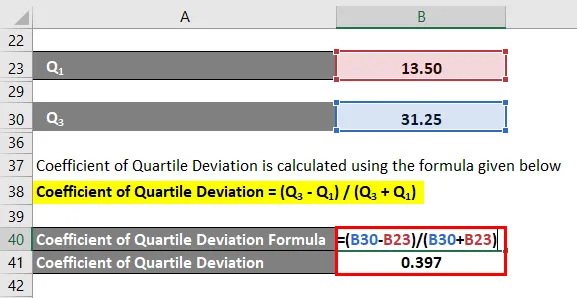
- Kvartiili kõrvalekalde koefitsient = (31, 25–13, 50) /(31, 25 + 13, 50)
- Kvartiili kõrvalekalde koefitsient = 0. 397
Kvartiili kõrvalekalde valem - näide nr 2
Järgnevalt on esitatud vaatlused kaubanduskeskuse ühepäevase müügi kohta, kus määrame esimese 50 erineva vanuserühma kliendi sageduse. Nüüd peame arvutama kvartiili kõrvalekalde ja kvartiili kõrvalekalde koefitsiendi.

Lahendus:
Sagedusjaotuse korral saab kvartiile arvutada järgmise valemi abil:
Q i = l + (h / f) * (i * (N / 4) - c) ; i = 1, 2, 3
Kus,
- l = kvartiilrühma alumine piir
- h = kvartiilrühma laius
- f = kvartiilrühma sagedus
- N = vaatluste koguarv
- c = kumulatiivne sagedus
Esiteks peame arvutama kumulatiivse sagedustabeli
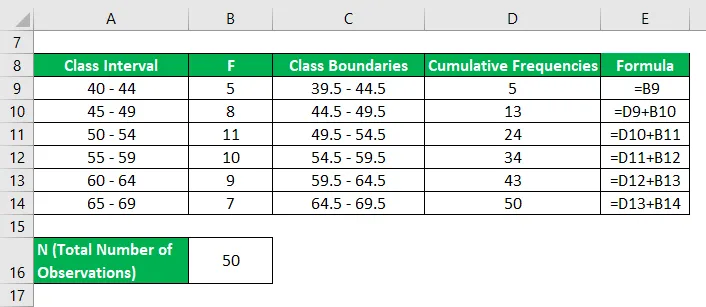
Esimene kvartiil (Q 1 ) arvutatakse järgmise valemi abil
Esimene kvartiil ( 1. kvartal)
Q i = (i * (N) / 4) th obstruktsioon
- Q 1 = (1 * (50) / 4) th obstruktsioon
- Q 1 = 12, 50 th obesvation
Alates 12.50 on väärtus vahemikus 44, 5 - 49, 5
Seetõttu on I kvartali grupp (44, 5–49, 5)
Q i = l + (h / f) * (i * (N / 4) - c)
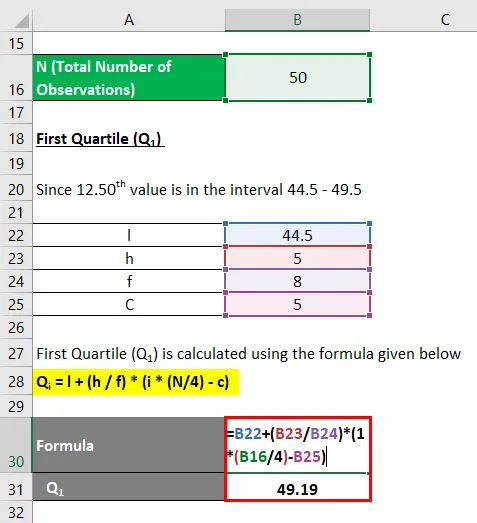
- Q 1 = (44, 5 + (5/8) * (1 * (50/4) - 5)
- Q1 = 44, 5 + 4, 6875
- Q 1 = 49, 19
Kolmas kvartiil (Q 3 ) arvutatakse järgmise valemi abil
Kolmas kvartiil (Q 3 )
Q i = (i * (N) / 4) th obstruktsioon
Q1 = (i * (N) / 4) th obstruktsioon
- Q3 = (3 * (50) / 4) th obstruktsioon
- Q 3 = 37, 50 th obesvation
Kuna väärtus 37.50 on vahemikus (59.5–64.5)
Seetõttu on Q3 rühm (59, 5–64, 5)
Q i = l + (h / f) * (i * (N / 4) - c)
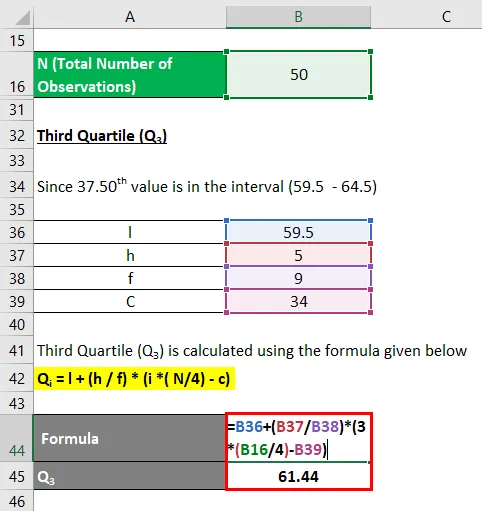
- Q 3 = 59, 5 + (5/9) * (3 * (50/4) - 34)
- Q 3 = 59, 5 + 1, 944
- Q 3 = 61, 44
Pannes väärtused kvartiili kõrvalekalde ja kvartiili kõrvalekalde koefitsientide valemitesse, saame:
Kvartiili kõrvalekalle arvutatakse järgmise valemi abil
Kvartiili hälve = (Q 3 - Q 1 ) / 2
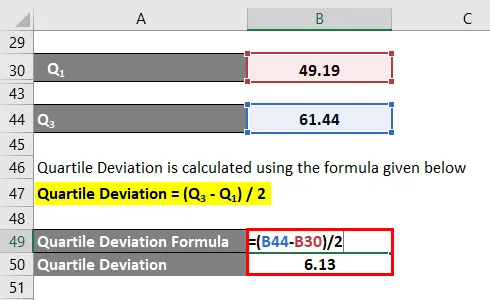
- Kvartiili kõrvalekalle = (61, 44 - 49, 19) / 2
- Kvartiili hälve = 6.13
Kvartiili kõrvalekalde koefitsient arvutatakse järgmise valemi abil
Kvartiili kõrvalekalde koefitsient = (Q 3 - Q 1 ) / (Q 3 + Q 1 )
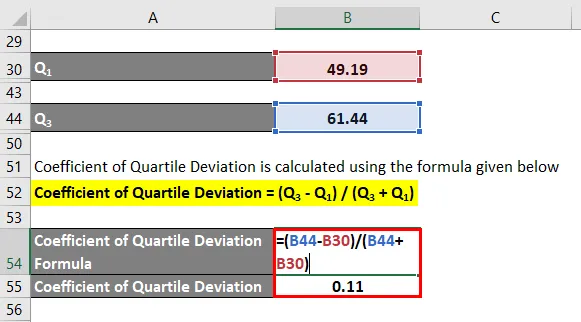
- Kvartiili kõrvalekalde koefitsient = (61, 44 - 49, 19) / (61, 44 + 49, 19)
- Kvartiili kõrvalekalde koefitsient = 12, 25 / 110, 63
- Kvartiili kõrvalekalde koefitsient = 0, 11
Seletus
Kvartiilne hälve on dispersioon andmete keskel, kus see määratleb andmete leviku. Nagu me teame, nimetatakse kolmanda kvartiili ja esimese kvartiili erinevust kvartiilidevaheliseks vahemikuks ja pooltevahelist kvartiilide vahemikku nimetatakse Semi-kvartiilide vahemikuks, mida nimetatakse ka kvartiili hälbeks. Nüüd saame arvutada kvartaalse hälbe nii grupeeritud kui ka grupeerimata andmete jaoks, kasutades allpool esitatud valemit.
Kvartiili hälve = (kolmas kvartiil - esimene kvartiil) / 2
Kvartiili hälve = (Q 3 - Q 1 ) / 2
Kuigi kahe andmekogumi vahelise variatsiooni võrdlemiseks kasutatakse kvartiili hälbe koefitsienti .6868 Lisaks ei mõjuta kvartiilset kõrvalekallet äärmuslikud väärtused, kui see sisaldab äärmuslikke väärtusi. Sel viisil saab arvutada kvartiili kõrvalekalde koefitsiendi.
Kvartiili kõrvalekalde koefitsient = (Q 3 - Q 1 ) / (Q 3 + Q 1 )
Kvartiili hälbe ja kvartiili koefitsiendi kontseptsiooni saab selgitada näite abil kindla sammuga.
1. samm: hankige rühmitamata andmete komplekt
Probleemikirjelduses oleme kaalunud lööja poolt 20 viimase katsevõistluse läbimist: 96, 70, 100, 89, 78, 56, 45, 78, 68, 42, 66, 89, 90, 54, 44, 67, 87, 90, 97 ja 98
2. samm : korraldage andmed kasvavas järjekorras:
42, 44, 45, 54, 56, 66, 67, 68, 70, 78, 78, 87, 89, 89, 90, 92, 96, 97, 98, 100
Esimene kvartiil ( 1. kvartal )
Arvutage esimene kvartiil
Q i = i * (n + 1) / 4- ne obstruktsioon
- Q 1 = 1 * (20 + 1) / 4- ne obstruktsioon
- Q 1 = 5, 25 th obesvation
Niisiis, 5, 25 vaatlus jääb järjestatud rühmas 5. ja 6. väärtuse vahele või seega vahemikku 55–66
- K 1 = 55 + 0, 25 * (66–55)
- Q 1 = 55 + 2, 75
- Q 1 = 57, 25
Kolmas kvartiil (Q 3 )
Kolmas kvartiil arvutatakse järgmiselt:
Q i = i * (n + 1) / 4-ne obstruktsioon
- Q 3 = i * (n + 1) / 4
- Q 3 = 3 * (20 + 1) / 4. vaatlus
- Q 3 = 15, 75 vaatlus
Kus 15, 75 on vahemikus 15 kuni 16 väärtus tellitud rühmas
15. vaatlus = 90
16. obstruktsioon = 96
- Q3 = 90 +0, 75 * (96–90)
- Q3 = 90 + 4, 5
- Q3 = 94, 5
3. samm : kvartiilhälbe ja kvartiili kõrvalekalde koefitsiendi arvutamine vastava tulemuse põhjal.
Kvartiili hälve = (Q 3 - Q 1 ) / 2
- Kvartiili kõrvalekalle = (94, 5 - 57, 25) / 2
- Kvartiili kõrvalekalle = 18, 625
Kvartiili kõrvalekalde koefitsient = (Q 3 - Q 1 ) / (Q 3 + Q 1 )
- Kvartiili kõrvalekalde koefitsient = (94, 5 - 57, 25) / (94, 5 +57, 25)
- Kvartiili kõrvalekalde koefitsient = 0, 2454
Kvartiilhälbe valemi olulisus ja kasutamine
- Kvartiili kõrvalekalle ei arvesta jaotuse palju äärmuslikumaid punkte.
- QD muutub ka seoses andmete mahu muutumisega.
- See on parim mõõta avatud süsteemi jaoks.
- Vähem mõjutatud on valimite kõikumised andmekogumis
- Ainult sõltuvad jaotuse kesksetest väärtustest.
Kvartiili kõrvalekalde valemi kalkulaator
Võite kasutada järgmist kvartiilhälbe valemi kalkulaatorit
| Q 3 | |
| Q 1 | |
| Kvartiilne kõrvalekalle | |
| Kvartili hälve = |
|
|
Soovitatavad artiklid
See on kvartiili kõrvalekalde valemi juhend. Siin arutatakse, kuidas kvartaalse hälbe valemit arvutada koos praktiliste näidetega. Pakume ka kvartaalse kõrvalekalde kalkulaatorit koos allalaaditava excelimalliga. Lisateabe saamiseks võite vaadata ka järgmisi artikleid -
- Reaalse intressimäära valemi näide
- Müügitulu valem
- Turuosa valem
- Kuidas arvutada netomüüki?