Mis on GLM R-s?
Üldistatud lineaarsed mudelid on lineaarsete regressioonimudelite alamhulk ja toetab tõhusalt mitte-normaalseid jaotusi. Selle toetamiseks on soovitatav kasutada funktsiooni glm (). GLM töötab muutujaga hästi, kui dispersioon ei ole konstantne ja jaotub normaalselt. Määratletakse lingifunktsioon, et muuta vastuse muutuja sobivaks sobivaks mudeliks. LM mudel tehakse nii perekonna kui ka valemiga. GLM-mudelil on kolm võtmekomponenti, mida nimetatakse juhuslikuks (tõenäosus), süstemaatiliseks (lineaarne ennustaja), lingikomponendiks (funktsioon logit). Glm kasutamise eeliseks on see, et neil on mudeli paindlikkus, pole vaja pidevat dispersiooni ja see mudel sobib maksimaalse tõenäosuse hindamiseks ja selle suhetega. Selles teemas hakkame RM-i kohta tundma õppima.
GLM funktsioon
Süntaks: glm (valem, perekond, andmed, kaalud, alamhulk, algus = null, mudel = TRUE, meetod = ””…)
Perekonnatüübid (kaasa arvatud mudelitüübid) hõlmavad siin binoomi, Poissoni, Gaussi, gammat, kvaasi. Igal jaotusel on erinev kasutus ja seda saab kasutada nii klassifitseerimisel kui ka ennustamisel. Ja kui mudel on gaussiline, peaks vastus olema tõeline täisarv.
Ja kui mudel on binoomne, peaks vastus olema binaarsete väärtustega klassid.
Ja kui mudeliks on Poisson, peaks vastus olema arvandmetega mittenegatiivne.
Ja kui mudel on gamma, peaks vastus olema positiivne arvväärtus.
glm.fit () - mudeli sobitamiseks
Lrfit () - tähistab logistilist taandarengut.
update () - aitab mudeli värskendamisel.
anova () - selle test on valikuline.
Kuidas luua GLM R-is?
Siin näeme, kuidas funktsiooni glm () abil luua binaarsete andmetega lihtne üldistatud lineaarne mudel. Ja jätkates Trees andmekoguga.
Näited
// Teegi importiminelibrary(dplyr)
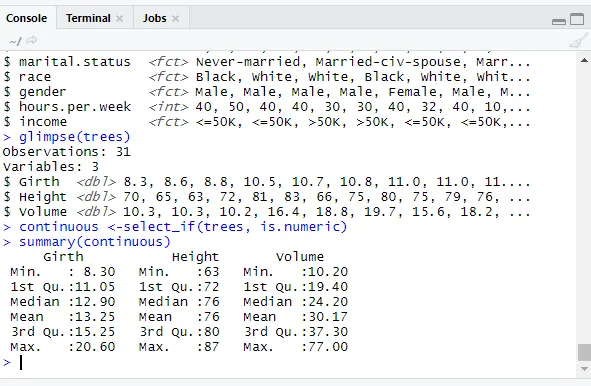
glimpse(trees)

Kategooriliste väärtuste nägemiseks määratakse tegurid.
levels(factor(trees$Girth))
// Pidevate muutujate kontrollimine
library(dplyr)
continuous <-select_if(trees, is.numeric)
summary(continuous)
// Kaasa arvatud puu andmestik R-otsingu Pathattachis (puud)
x<-glm(Volume~Height+Girth)
x
Väljund:
| Kõne: glm (valem = maht ~ kõrgus + ümbermõõt)
Koefitsiendid: Kõrgus ümbermõõt -57.9877 0.3393 4.7082 Vabadusastmed: 30 kokku (st null); 28 jääk Null Deviance: 8106 Järelejäänud hälve: 421, 9 AIC: 176, 9 |
summary(x)
| Helistama:
glm (valem = maht ~ kõrgus + ümbermõõt) Deviance'i jäägid: Min 1Q mediaan 3Q max -6, 4065 -2, 6493 -0, 2876 2, 2003 8, 4847 Koefitsiendid: Hinnanguline Std. Viga t väärtus Pr (> | t |) (Pealtkuulamine) -57.9877 8.6382 -6.713 2.75e-07 *** Kõrgus 0.3393 0.1302 2.607 0.0145 * Ümbermõõt 4, 7082 0, 2643 17, 816 <2e-16 *** - Signif. koodid: 0 '***' 0, 001 '**' 0, 01 '*' 0, 05 '.' 0, 1 '' 1 (Gaussi perekonna dispersiooniparameeter on 15, 06862) Nullhälve: 8106, 08 30-le vabadusastmele Jääkkalle: 421, 92 28 vabadusastmel AIC: 176, 91 Fisheri punktide iteratsioonide arv: 2 |
Kokkuvõtliku funktsiooni väljund annab välja kõned, koefitsiendid ja jäägid. Ülaltoodud vastusest selgub, et nii kõrguse kui ka ümbermõõdu koefitsiendid on ebaolulised, kuna nende tõenäosus on väiksem kui 0, 5. Ja hälvet on kahel variandil, mida nimetatakse nulliks ja jäägiks. Lõpuks on kalurite punktisüsteem algoritm, mis lahendab maksimaalse tõenäosusega seotud probleemid. Binoomi korral on vastuseks vektor või maatriks. cbind () kasutatakse veeruvektorite sidumiseks maatriksis. Ja selleks, et saada üksikasjalikku teavet sobivuse kokkuvõttest.
Selleks nagu kapoti test, käivitatakse järgmine kood.
step(x, test="LRT")
Start: AIC=176.91
Volume ~ Height + Girth
Df Deviance AIC scaled dev. Pr(>Chi)
421.9 176.91
- Height 1 524.3 181.65 6.735 0.009455 **
- Girth 1 5204.9 252.80 77.889 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Call: glm(formula = Volume ~ Height + Girth)
Coefficients:
(Intercept) Height Girth
-57.9877 0.3393 4.7082
Degrees of Freedom: 30 Total (ie Null); 28 Residual
Null Deviance: 8106
Residual Deviance: 421.9 AIC: 176.9
Mudel sobib
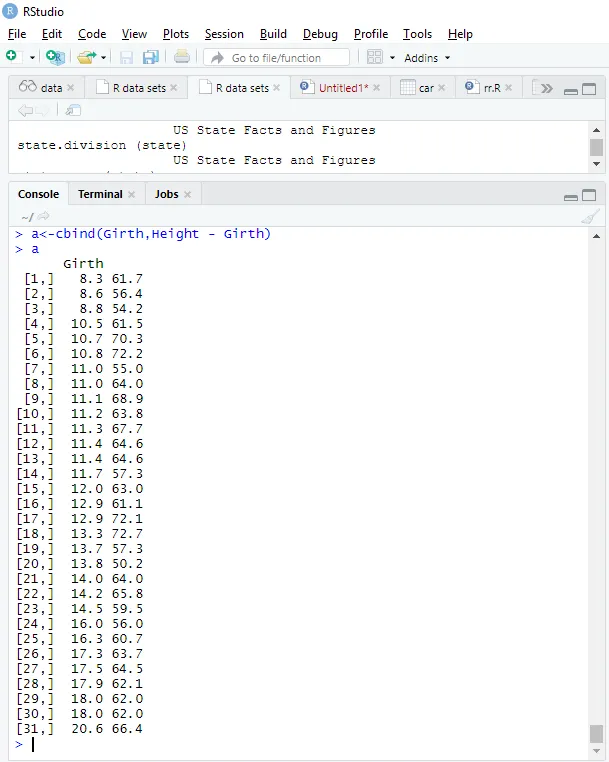
a<-cbind(Height, Girth - Height)
> a
kokkuvõte (puud)
Girth Height Volume
Min. : 8.30 Min. :63 Min. :10.20
1st Qu.:11.05 1st Qu.:72 1st Qu.:19.40
Median :12.90 Median :76 Median :24.20
Mean :13.25 Mean :76 Mean :30.17
3rd Qu.:15.25 3rd Qu.:80 3rd Qu.:37.30
Max. :20.60 Max. :87 Max. :77.00
Sobiva standardhälbe saamiseks
apply(trees, sd)
Girth Height Volume
3.138139 6.371813 16.437846
predict <- predict(logit, data_test, type = 'response')
Järgmisena viidatakse loendusvastuse muutujale hea reageerimise sobivuse modelleerimiseks. Selle arvutamiseks kasutame andmebaasi USAccDeath.
Sisestagem R-konsooli järgmised katkendid ja vaatame, kuidas nende kohta aastaarvestust ja aastaruutu täidetakse.
data("USAccDeaths")
force(USAccDeaths)
// Analüüsida aastat 1973–1978.
disc <- data.frame(count=as.numeric(USAccDeaths), year=seq(0, (length(USAccDeaths)-1), 1)))
yearSqr=disc$year^2
a1 <- glm(count~year+yearSqr, family="poisson", data=disc)
summary(a1)
| Helistama:
glm (valem = arv ~ aasta + aastaSqr, perekond = "poisson", andmed = ketas) Deviance'i jäägid: Min 1Q mediaan 3Q max -22, 4344 -6, 4401 -0, 0981 6, 0508 21, 4578 Koefitsiendid: Hinnanguline Std. Viga z väärtus Pr (> | z |) (Pealtkuulamine) 9.187e + 00 3.557e-03 2582.49 <2e-16 *** aasta -7.207e-03 2.354e-04 -30.62 <2e-16 *** yearSqr 8.841e-05 3.221e-06 27.45 <2e-16 *** - Signif. koodid: 0 '***' 0, 001 '**' 0, 01 '*' 0, 05 '.' 0, 1 '' 1 (Poissoni perekonna dispersiooniparameeter võetakse 1) Nullhälve: 7357, 4 71 vabadusastmel Jääkkalle: 6358, 0 69 vabadusastmel AIC: 7149, 8 Fisheri punktide iteratsioonide arv: 4 |
Mudeli sobivuse kontrollimiseks võib leidmiseks kasutada järgmist käsku
katse jäägid. Allpool toodud tulemuse järgi on väärtus 0.
1 - pchisq(deviance(a1), df.residual(a1))
QuasiPoissoni perekonna kasutamine antud andmete suurema variatsiooni saavutamiseks
a2 <- glm(count~year+yearSqr, family="quasipoisson", data=disc)
summary(a2)
| Helistama:
glm (valem = arv ~ aasta + aastaSqr, perekond = "kvaasipoisson", andmed = ketas) Deviance'i jäägid: Min 1Q mediaan 3Q max -22, 4344 -6, 4401 -0, 0981 6, 0508 21, 4578 Koefitsiendid: Hinnanguline Std. Viga t väärtus Pr (> | t |) (Pealtkuulamine) 9.187e + 00 3.417e-02 268.822 <2e-16 *** aasta -7.207e-03 2.261e-03 -3.188 0.00216 ** yearSqr 8.841e-05 3.095e-05 2.857 0.00565 ** - (Quasipoissoni perekonna dispersiooniparameeter on 92, 28857) Nullhälve: 7357, 4 71 vabadusastmel Jääkkalle: 6358, 0 69 vabadusastmel AIC: NA Fisheri punktide iteratsioonide arv: 4 |
Poissoni võrdlus binomiaalse AIC väärtusega erineb oluliselt. Neid saab analüüsida täpsuse ja tagasikutsumise suhtega. Järgmine samm on kontrollida, et jääkide dispersioon oleks keskmisega proportsionaalne. Siis saame proovida, kasutades mudeli parendamiseks ROCR-i teeki.
Järeldus
Seetõttu oleme keskendunud erimudelile, mida nimetatakse üldistatud lineaarseks mudeliks, mis aitab mudeli parameetrite fokuseerimisel ja hindamisel. See on peamiselt pideva reageerimise muutuja potentsiaal. Ja me oleme näinud, kuidas glm sobib R sisseehitatud pakettidega. Need on kõige populaarsemad lähenemisviisid loendusandmete mõõtmiseks ja tugev vahend klassifitseerimistehnikate jaoks, mida andmeteadlane kasutab. R-keel aitab muidugi keerukate matemaatiliste funktsioonide tegemisel
Soovitatavad artiklid
See on juhend GLM-i kohta R. Siin käsitleme GLM-i funktsiooni ja kuidas luua GLM-i koos puude andmekogumite näidete ja väljundiga. Lisateabe saamiseks võite vaadata ka järgmist artiklit -
- R programmeerimiskeel
- Suurandmete arhitektuur
- Logistiline regressioon R-s
- Suurandmete analüüsi töökohad
- Poissoni regressioon R | Poissoni regressiooni rakendamine