Matlabi vektorid - Vektorite töö tüübid koos näidetega

Sissejuhatus Matlabi vektoritesse

Vektor on suletud elementide komplekt. Matlabis saame vektoreid luua nurksulgude abil. Vektorid on üks massiivide illustratsioonidest (ühemõõtmeline massiiv). seda saab esitada kahel viisil ridavektorina ja veeruvektorina.

Ridavektor

See on horisontaalne elementide komplekt. See on esitatud nurksulgudes. Iga element eraldatakse koma või tühikuga.

X = (4 7 8) või X = (4, 7, 8)

Veeruvektor

See on vertikaalne elementide komplekt. See on esindatud ka nurksulgudes. Veervektorite loomiseks on kahel viisil esiteks üksteisest eraldamine semikooloniga ja teine viis - iga elemendi kirjutamine käsuakna järgmisele reale.

X = (4; 6; 7) või

X = (4

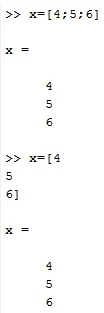
Vektorioperatsioonid

Vektorvedajad jagatakse laias laastus kahte kategooriasse.

1. Aritmeetiline operatsioon

Vaatleme kahte vektorit x ja y väärtustega x = (1 4 5 3) ja y = (5 3 2 1), saame nende kahe vektori x ja y abil teha mitmesuguseid toiminguid.

a. Korrutamine: Seda funktsiooni kasutatakse kogu vektori aritmeetilise väärtuse korrutamiseks.

Näiteks:

mul = 3 * x

mul = 3 * (1 4 5 3)

mul = (3 12 15 9)

Süntaks: variable name = arithmetic constant * vector name

b. Trigonomeetriline funktsioon: me saame rakendada mis tahes trigonomeetrilist funktsiooni vektoritaolisele sin, cos, tan, cosec, sec jne.

Näide tri = cos (x)

Vastus on: 0, 54–0, 65 0, 28–0, 99

Süntaks: variable name = trigonometric function name ( vector name )

Summa: see näitab tervete elementide kokku (liitmist) ühes vektoris.

Näide

x = (1 4 5 3)

Kokku = summa (x)

Väljund kokku = 13

Süntaks: variable name = = sum ( vector name )

c. Pikkus: see näitab konkreetse vektori pikkust. Olgem üks vektor p = (9 7 5 3 1 9 7 5 3 1)

Näide

p = (9 7 5 3 1 9 7 5 3 1)

Len = pikkus (p)

Väljund on Len = 10

d. Vektorite lisamine: kahe või mitme vektori lisamine on Matlabis lihtne toiming, kaalugeme kahte vektorit p ja q.

P = (4 6 3 2) ja q = (5 7 9 1)

Lisage = p + q

Väljund on Lisa = (9 13 12 3)

Süntaks: vector name operator ( + ) vector name

Samamoodi saame lahutamise toiminguid teha näiteks sub = p - q

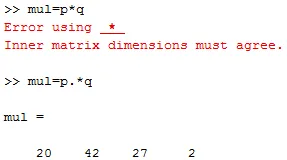
e. Vektorite korrutamine: Kui tahame teha kahe vektori korrutamise, siis lihtne korrutamisoperaator (*) ei tööta. Seetõttu peame lisama punktioperaatori ('.') Koos korrutusega operaatoriga.

Näide:

P = (4 6 3 2) ja q = (5 7 9 1)

mul = lk. * q

väljund on mul = (20 42 27 2)

Süntaks: variable name = vector name dot operator multiplication operator vector name

Oletame, et tahan teada saada ühe konkreetse vektori ruudu või tahan vektori korrutada ainult selle vektoriga.

Siis on süntaksiks squr = x. 2

2. Suhteline operatsioon

a. Võrdne operaatoriga : see operaator võrdleb iga n elementi kahe vektoriga ja annab väljundi nullina ja ühe vormiga.

Näide

m = (2 5 8)

Ja n = (5 5 3)

Nagu me teame, vektoris m ja vektoris n on kolm elementi,

m == n

Ülaltoodud avaldus annab väljundi kujul 0 1 0, mis tähendab, et esimene ei ole võrdne, teine arv on võrdne ja kolmas ei ole võrdne. O tähistab valet ja 1 tähistab õiget.

b. Vähem kui operaator (<): vähem kui operaator tähistab sümboliga <<. saame võrrelda antud maatriksit mis tahes aritmeetilise konstandiga või mis tahes muu vektoriga.

Näide

m = (3 2 4)

n = (1 1 1)

m <n

väljund on 0 0 0, see tähendab, et kõik arvud on suuremad kui vektor n.

ja kui m <10

siis on väljund 1 1 1, see tähendab, et kõik numbrid on alla 10.

c. Suurem kui operaator (>): suurem kui operaator tähistab sümboliga ('>'). Saame antud maatriksit võrrelda mis tahes aritmeetilise konstandiga või mis tahes muu vektoriga.

Näide:

M = (3 2 4)

N = (1 1 1)

m> n

Väljund on 1 1 1, see tähendab, et kõik väärtused on suuremad kui vektori n väärtused.

Järeldus - vektorid Matlabis

Matlabis saame luua erinevat tüüpi vektoreid, kus saame teostada mitmesuguseid toiminguid, nagu liitmine, lahutamine, korrutamine, ruut, ruutjuur, võimsus, skaleerimine, vektorite korrutamine, punktkorrutus jne.

Soovitatavad artiklid

See on Matlabis tegutseva Vektorite juhend. Siin käsitleme vektoroperatsioonide tüüpe, mis hõlmavad aritmeetilist ja relatsioonilist operatsiooni, koos mõnede näidetega. Lisateabe saamiseks võite vaadata ka järgmisi artikleid -