
Geomeetrilise jaotuse valem (sisukord)
- Valem
- Näited
- Kalkulaator
Mis on geomeetrilise jaotuse valem?
Statistikas ja tõenäosusteoorias öeldakse, et juhuslikul muutujal on geomeetriline jaotus ainult siis, kui selle tõenäosustiheduse funktsiooni saab väljendada edu tõenäosuse ja uuringute arvu funktsioonina. Tegelikult aitab geomeetriline jaotus edukuse esmakordse esinemise tõenäosuse kindlaksmääramisel pärast teatud arvu katseid, arvestades õnnestumise tõenäosust. Kui õnnestumise tõenäosus on „p”, saab edukuse esmakordse esinemise tõenäosuse valemi tuletada pärast „k” -katseid, korrutades õnnestumise tõenäosuse ühega miinus õnnestumise tõenäosusega, mis tõstetakse mitme kohtuprotsessid miinus üks. Matemaatiliselt on tõenäosustiheduse funktsioon esitatud järgmiselt:
P(X=k) = p * (1 – p) (k – 1)
Kus,
- p = edu tõenäosus
- k = proov, kus esimene edu saavutatakse
Geomeetrilise jaotuse valemi näited (Exceli malliga)
Võtame näite, et mõista paremini geomeetrilise jaotuse arvutamist.
Selle geomeetrilise jaotuse valemi Exceli malli saate alla laadida siit - geomeetrilise jaotuse valemi Exceli mallGeomeetrilise jaotuse valem - näide # 1
Võtame näiteks lööja, kes ei suutnud esimesed seitse palli maha lüüa, vaid tabas kaheksanda kättetoimetamise piiri, millega ta silmitsi oli. Kui lööja tõenäosus lüüa piiri on 0, 25, arvutage tõenäosus, et lööja lööb kaheksa palli järel esimest piiri.

Lahendus:
Tõenäosus arvutatakse järgmise geomeetrilise jaotuse valemi abil
P = p * (1 - p) (k - 1)
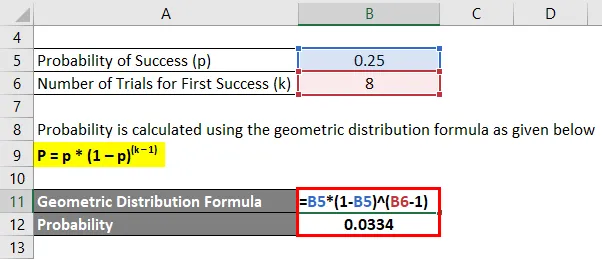
- Tõenäosus = 0, 25 * (1 - 0, 25) (8 - 1)
- Tõenäosus = 0, 0334
Seetõttu on 0, 0334 tõenäosus, et lööja tabab kaheksa palli järel esimest piiri.
Geomeetrilise jaotuse valem - näide # 2
Liigume nüüd jalgpalli spordi juurde ja võtame näiteks jalgpalluri, kes lööb värava tõenäosusega 0.7, kui ta palli endale saab. Määrake tõenäosus, et jalgpallur lööb oma esimese värava pärast:
- 8 katset
- 6 katset
- 4 katset
- 2 katset

Lahendus:
8 katset
Tõenäosus arvutatakse järgmise geomeetrilise jaotuse valemi abil
P = p * (1 - p) (k - 1)
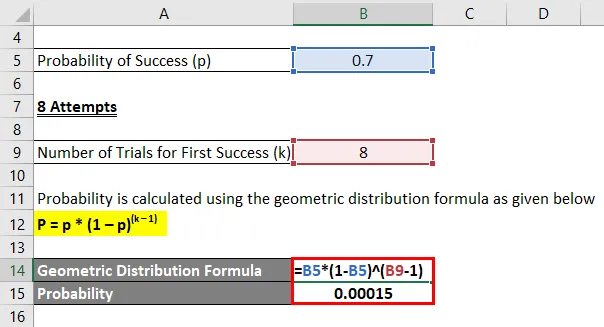
- Tõenäosus = 0, 7 * (1–0, 7) (8–1)
- Tõenäosus = 0, 00015
6 katset
Tõenäosus arvutatakse järgmise geomeetrilise jaotuse valemi abil
P = p * (1 - p) (k - 1)
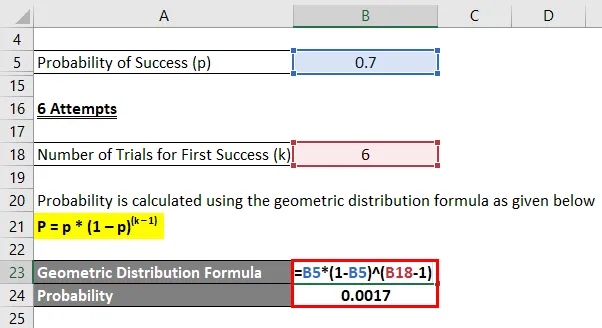
- Tõenäosus = 0, 7 * (1 - 0, 7) (6 - 1)
- Tõenäosus = 0, 0017
4 katset
Tõenäosus arvutatakse järgmise geomeetrilise jaotuse valemi abil
P = p * (1 - p) (k - 1)
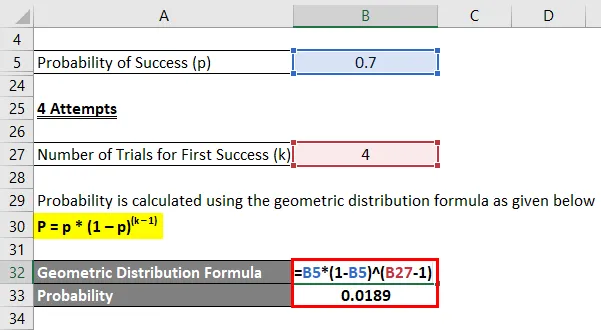
- Tõenäosus = 0, 7 * (1–0, 7) ( 4–1 )
- Tõenäosus = 0, 0189
2 katset
Tõenäosus arvutatakse järgmise geomeetrilise jaotuse valemi abil
P = p * (1 - p) (k - 1)
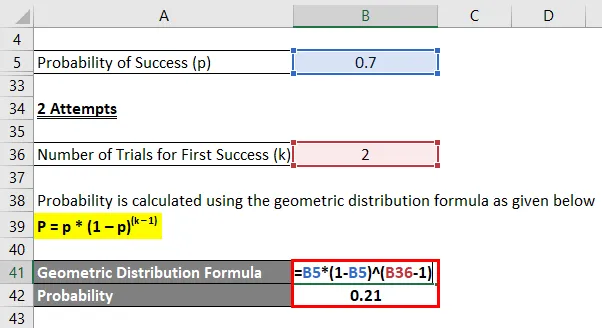
- Tõenäosus = 0, 7 * (1 - 0, 7) (2 - 1)
- Tõenäosus = 0, 21
Seetõttu võib ülaltoodud näites näha, et esimese õnnestumise tõenäosus väheneb ebaõnnestunud katsete arvu suurenemisega, st esimese õnnestumise tõenäosus langes 0, 21 peale 2 katset 0, 00015 peale 8 katset.
Seletus
Geomeetrilise jaotuse valem tuletatakse järgmiste sammude abil:
1. samm: kõigepealt määrake sündmuse õnnestumise tõenäosus ja seda tähistatakse tähega “p”.
2. samm. Järgmisena saab rikke tõenäosuse arvutada järgmiselt: (1 - p).
3. samm: seejärel määrake katsete arv, mille jooksul registreeritakse esimene õnnestumise esinemisaste või õnnestumise tõenäosus on võrdne ühega. Katsete arvu tähistatakse tähega k.
4. samm: Lõpuks saab k-katsete järgselt esimese edu tõenäosuse valemi tuletada, arvutades kõigepealt välja tõenäolised ebaõnnestumised, st (1 - p), mis tõstetakse ebaõnnestunud katsete arvule enne esimest edu, st (k - 1) ja seejärel korrutatakse tulemus k-nda katse eduga, nagu allpool näidatud.
P (X = k) = p * (1 - p) (k - 1)
Geomeetrilise jaotuse valemi olulisus ja kasutamine
Geomeetrilise jaotuse kontseptsiooni saab kasutada esimese õnnestumise tõenäosuse kindlaksmääramisel pärast teatud arvu katseid. Tegelikult on geomeetriline jaotusmudel negatiivse binoomjaotuse erijuhtum ja see on rakendatav ainult nende sõltumatute uuringute korral, kus igas uuringus on võimalik ainult kaks tulemust. Tuleb märkida, et vastavalt sellele jaotusmudelile väheneb ebaõnnestunud katsete arvu iga suurenemine esimese õnnestumise tõenäosuse korral märkimisväärselt. Sellistel juhtudel saab jaotust kasutada ebaõnnestumiste arvu kindlaksmääramiseks enne esimest õnnestumist.
Geomeetrilise jaotuse valemi kalkulaator
Võite kasutada järgmist geomeetrilise jaotuse kalkulaatorit
| lk | |
| k | |
| P (X = k) | |
| P (X = k) = | p * (1 - p) (k-1) |
| = | 0 * (1 - 0) (0-1) = 0 |
Soovitatavad artiklid
See on geomeetrilise jaotuse valemi juhend. Siin käsitleme kuidas arvutada geomeetrilist jaotust koos praktiliste näidetega. Pakume ka allalaaditava excelimalliga geomeetrilise jaotuse kalkulaatorit. Lisateabe saamiseks võite vaadata ka järgmisi artikleid -
- Mis on hüpergeomeetriline jaotusvalem?
- Poissoni jaotusvalemi näited
- T jaotusvalem (näited Exceli malliga)
- Tavalise normaaljaotuse valemi kalkulaator