
Lihtne intressimäära valem (sisukord)
- Lihtne intressimäära valem
- Lihtsa intressimäära valemi näited (Exceli malliga)
- Lihtne intressimäära kalkulaator
Lihtne intressimäära valem
Üldiselt võib öelda, et intress tähendab täiendavat summat, mida makstakse laenuandjalt rahalise abi saamiseks. Finantsperioodil, kui võtame laenu mingilt summalt mis tahes pangast või finantseerimisasutuselt, peame selle võimaluse koos selle täiendava summaga tagasi maksma. Sellist makstud lisatasu nimetatakse intressiks.
Intress võib olla erinevat tüüpi, näiteks lihtintress, liitintress, tegelik intress, aastane tootlus jne. Selles artiklis käsitleme lihtsat intressi.
Lihtsate intresside valem on üks lihtsamaid viise lühiajaliste laenude, ettemaksete ja tähtajaliste laenude intresside arvutamiseks. Lihtintressi korral arvutatakse intress laenusummalt, mida nimetatakse ka laenu põhisummaks. Sel juhul ei arvutata intressi laenusummalt kogunenud intressisummalt, sarnaselt liitintressi valemiga.
Lihtsa intressi arvutamiseks on vaja laenusummat koos laenuperioodi ja intressimääraga.
Lihtsa huvi valem on:
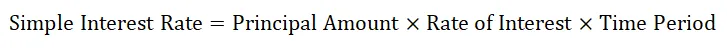
Seda valemit lühendatakse ka järgmiselt:
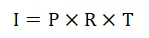
Kus,
- I = intressisumma
- P = laenusumma või laenatud summa
- R = lihtintressi määr
- T = laenu või ajahorisont
Lihtsa intressimäära valemi näited (Exceli malliga)
Mõistagem seda valemit mõne näite abil.
Selle lihtsa intressimääraga valemi Exceli malli saate alla laadida siit - lihtsa intressimääraga valemi Exceli mallLihtne intressimäära valem - näide nr 1
Ram võttis oma pankurilt laenu Rs.1000000 viieks aastaks. Intressimäär oli 5% aastas. Arvutage intressisumma ja tema kogukohustus 5. aasta lõpus.
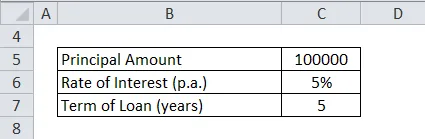
Niisiis, intressisumma, kasutades lihtsat intressimäära valemit, on järgmine:
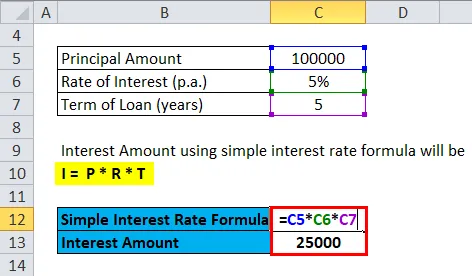
- I = P * R * T
- I = 100000 * 5% * 5
- I = Rs, 25000
Intressi suurus on Rs. 25000
Kogukohustus arvutatakse järgmiselt:
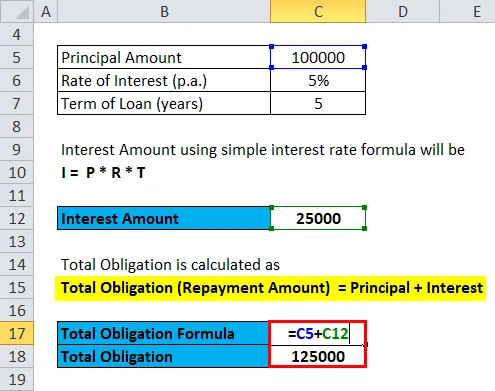
- Kohustus kokku (tagasimakse summa) = põhisumma + intress
- Tagasimaksesumma = 100000 + 25000
- Tagasimaksesumma = Rs. 125000
Lihtne intressimäära valem - näide nr 2
Ram ostis laenu eest müügikohast mobiiltelefoni Rs.20000. Laenu tingimused on järgmised:
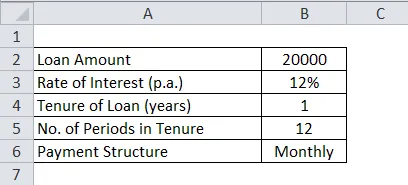
Arvutage ERI ja intressi summa perioodi kohta.
Siin
- P = 20000
- R = 12% aastas
- Aeg = 1 aasta
- Makseperioodide arv (N) = 12 kuus
Nii saab EMI ja intressisumma arvutada Excelis, kasutades PMT Function. Teise võimalusena võime EMI ja intressi arvutada ka valemi abil,
- EMI = (P * R * (1 + R) N ) / ((1 + R) N -1)
- EMI = (20000 * 12% * (1 + 12%) 12 ) / ((1 + 12%) 12 -1)
- EMI = Rs. 1776, 98
Valemi abil saame teada, et Ram peab 12 kuu jooksul maksma ERI-d Rs.1776.98 . Tema intressimakse iga perioodi kohta väheneb ja vastavalt suureneb järk-järgult põhiosa tagasimakse, mille tulemusel makstakse laenusumma koos intressidega 12 kuu lõpus täielikult välja.
Iga ERI ERI, põhimakse tagasimakse ja intressi arvutused on toodud allpool toodud joonisel:
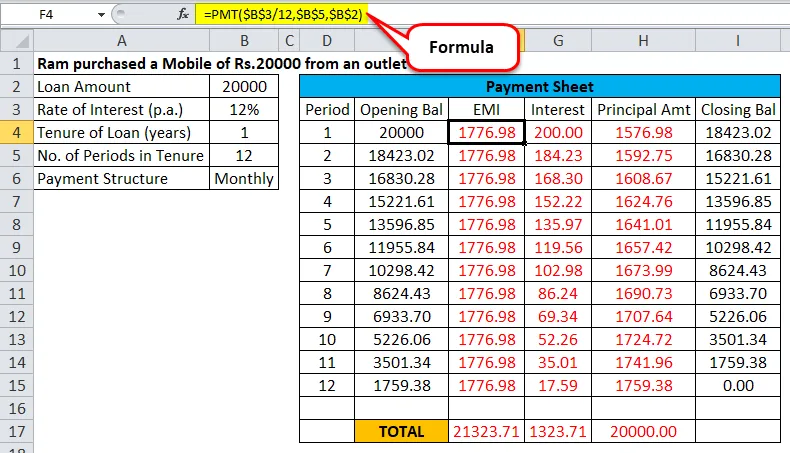
Nagu näeme, et EMI jääb samaks ja igakuise osamakse tagasimaksega väheneb ka laenu jääksumma ning muutub laenutähtaja lõppedes nulliks.
Lihtne intressimäära valem - näide nr 3
DHFL Ltd emiteeris kupongi kandva võlakirja väärtusega 100 000 Rs, mille intressimäär on 7% aastas. Võlakirja kasulik eluiga on 15 kuud, pärast mida võlakiri lunastatakse.
Investori teenitud intressi saab arvutada järgmiselt:
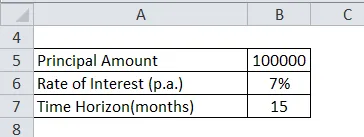
Intressi arvutamiseks peame viima intressimäära ja ajavahemiku sümmeetriasse. Niisiis,
Ajavahemik arvutatakse järgmiselt:
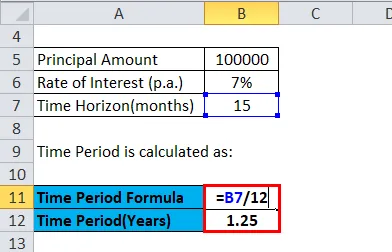
- Ajavahemik = 15/12 aastat
- Ajavahemik = 1, 25 aastat
Intressisumma, kasutades lihtsat intressimäära valemit, on järgmine:
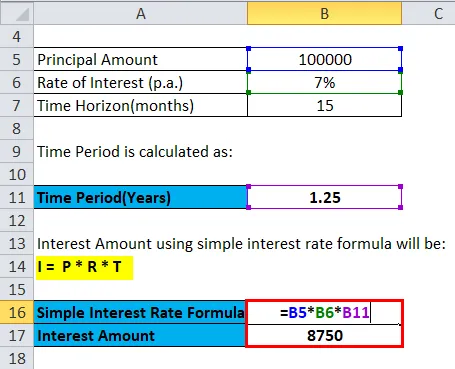
- I = P * R * T
- I = 100000 * 7% * 1, 25
- I = Rs, 8750
Seega on investori poolt lunastatava võlakirja pealt teenitud intress 8750 Rs .
Seletus
Intressimäära valem on kasulik laenusaaja intressikohustuse tundmisel võetud laenu eest ning see aitab ka laenuandjal nagu finantsasutused ja pangad välja arvutada antud abiga teenitud netointressitulu.
Lihtsa intressi arvutamisel tuleb meeles pidada, et intressimäär ja laenuperiood peaksid olema sümmeetrilised, st kui intressimäär on aastas, tuleb mitu perioodi väljendada ka aastaarvestuses. Ja kui ajavahemik on kuu / kvartal, tuleks intressimäär teisendada ka vastavalt kuu / kvartali sagedusele.
Selle valemi korral on intressi suurus laenu algperioodil kõrgem ja see väheneb järk-järgult kogu laenu kehtivusaja jooksul.
Lihtsa intressimäära valemi olulisus ja kasutamine
- See valem on üks lihtsamaid valemeid intressikohustuse arvutamiseks ja see ei võta arvesse liitintressi valemi omadusi, st intressi intressi.
- Seda valemit kasutatakse lühiajaliste laenude ja avansside ning laenude võtmise korral.
- Seda valemit kasutavad ka pangandussektorid hoiupangakontode ja lühiajaliste hoiuste intresside arvutamiseks.
- Autolaenude ja muude tarbijalaenude intressi arvutatakse ka lihtsa intressimäära valemi abil.
- Hoiuste sertifikaat (CD) on manustatud ka lihtsa intressimäära funktsiooniga.
- Võlakirjad maksavad ka lihtintressi kupongimakse näol.
Lihtne intressimäära kalkulaator
Võite kasutada järgmist lihtsat intressimäära kalkulaatorit
| Põhisumma | |
| Intressimäär | |
| Ajavahemik | |
| Lihtne intressimäära valem | |
| Lihtne intressimäära valem = | Põhisumma x Intressimäär x Ajavahemik |
| = | 0 x 0 x 0 = 0 |
Soovitatavad artiklid
See on juhend lihtsa intressimäära valemi koostamiseks. Siin käsitleme selle kasutamist koos praktiliste näidetega. Pakume teile ka lihtsat intressimäära kalkulaatorit koos allalaaditava excelimalliga. Lisateabe saamiseks võite vaadata ka järgmisi artikleid -
- Intresside kattearvu valem
- Netointressi marginaali arvutamine valemi abil
- Kuidas arvutada võla suhet?
- Puhaskasumi marginaali valem